数据结构——图
连通图
- 无向图
- 连通图 : 图中任意两点都连通
- 连通:如果从v到w存在一条(无向)路径,则称v和w是连通的
- **路径:**V到w的路径是一系列顶点{V,v1,V2,vn,w}的集合,其中任一对相邻的顶点间都有图中的边。路径的长度是路径中的边数(如果带权,则是所有边的权重和)。如果v到w之间的所有顶点都不同,则称简单路径
- ▲路径是边的超集,一条路径中可以有多条边
- 回路:起点等于终点的路径 ==> 有回路的路径为非简单路径
- 有向图:
- 强连通 : 有向图中顶点v和W之间存在双向路径,则称v和w是强连通的强连通图
- 强连通图 : 有向图中任意两顶点均强连通强连通分量:有向图的极大强连通子图
- 弱连通图 : 将有向图中边的方向擦去,能变成连通图的图叫 弱连通图
图不连通咋办?
- 非连通图
- 无向图
- 连通分量: 无向图的极大连通子图
- 极大顶点数 : 再加1个顶点就不连通了
- 极大边数 : 包含子图中所有顶点相连的所有边
- 连通分量: 无向图的极大连通子图
- 无向图
图的边可以是具有某种属性的对象: 007案例中的岸边
最小代价生成树
基础概念
最小生成树问题 : 村村通—> 使图连通的( 最少的边 \ 花销最小的 )
- 树
- 连通的
- 无回路
- V个顶点 , v-1条边
- 生成
- 包含所有的顶点
- V-1条边都在图里
- 任意加一条边都会构成回路
- 最小
- 边的权重和最小
▲ 最小代价生成树不存在 <----> 图不连通
贪心算法:
-
贪: 每一步是最好的
-
好: 权重是最小的
-
约束:
- 只能用图里有的边
- 正好用掉 v-1条边
- 不能有回路
算法实现:
Prim算法——让小树成长:

kruskal——将森林合并成树:
更贪心,直接将权重最小的边收进来

拓补排序
AOV
以顶点来表示活动。 一个活动是另一个活动的先决条件
不断抹去 没有前驱顶点(入度为0) 的顶点

提倡的做法: 将入度为0的顶点放到容器中

▲.这种方法还可以用来检测是不是有向无环图(DAG)
关键路径
AOE:
一般用于安排项目的工序
由绝不允许延误的活动组成的路径
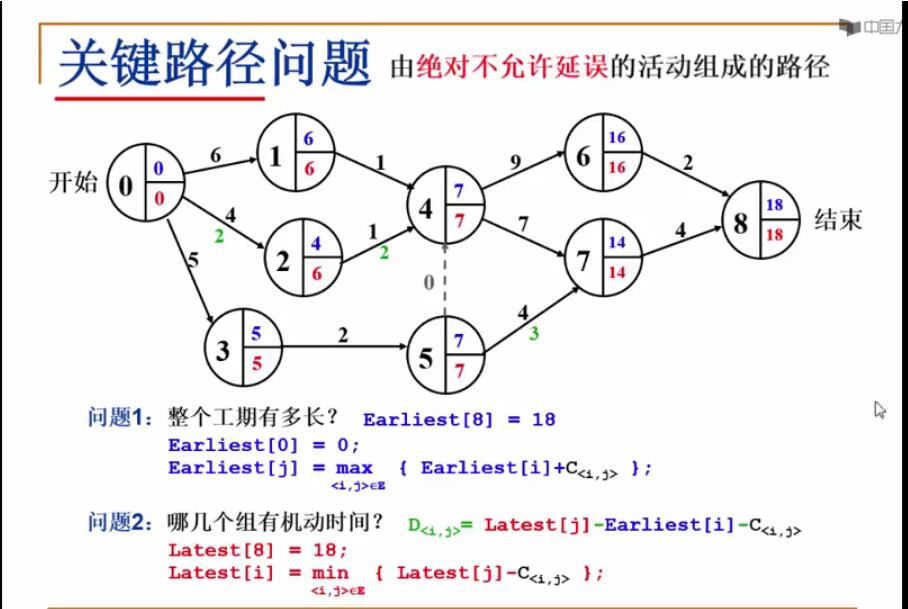
关键路径长度: earliest(n)
没有机动时间的路径为关键路径
Author: Mrli
Link: https://nymrli.top/2018/12/16/数据结构——图/
Copyright: All articles in this blog are licensed under CC BY-NC-SA 3.0 unless stating additionally.