ACM_动态规划

图解动态规划 : http://www.sohu.com/a/153858619_466939

动态规划 :

• 最优子结构
• 边界
• 状态转移方程式

题目二： 国王和金矿

有一个国家发现了5座金矿，每座金矿的黄金储量不同，需要参与挖掘的工人数也不同。参与挖矿工人的总数是10人。每座金矿要么全挖，要么不挖，不能派出一半人挖取一半金矿。要求用程序求解出，要想得到尽可能多的黄金，应该选择挖取哪几座金矿？

解法一: 排列组合

时间复杂度 : O(2^N)

解法二 : DP

1.找到最优子结构

• 10人4金矿(有一个金矿没挖)
• 10-3人4金矿(挖了一个金矿)

2.最优选择

5个金矿的最优选择，就是*（前4座金矿10工人的挖金数量）和（前4座金矿7工人的挖金数量+第5座金矿的挖金数量）*的最大值！

3.边界

---

经过整理可得 状态转移方程式:

• 边界:

F(n,w) = 0 (n<=1, w<p[0]);

F(n,w) = g[0] (n==1, w>=p[0]);

• 推导式

F(n,w) = F(n-1,w) (n>1, w<p[n-1])

F(n,w) = max(F(n-1,w), F(n-1,w-p[n-1])+g[n-1]) (n>1, w>=p[n-1])

实现方法:

简单递归

记忆搜索法

动态规划(递推式)

---

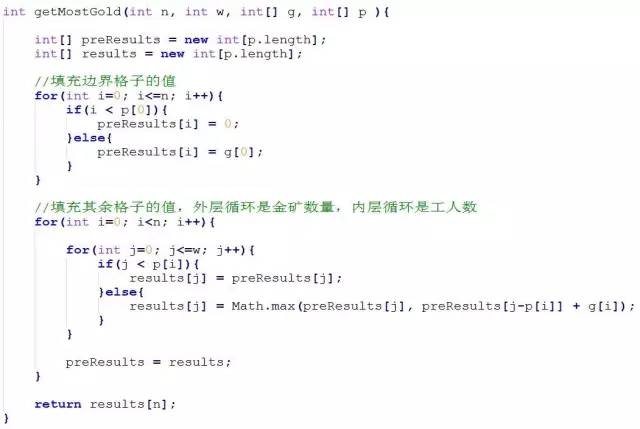
01背包问题

简单递归

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e4;
/* 01背包问题 */
pair<int,int> wv[maxn];
int N; // 物品数量
int W; // 背包重量


int rec(int i,int j){
    int res = 0;
    if( i == N) res= 0;
    else if( j < wv[i].first )
        res = rec(i+1,j);
    else res = max(rec(i+1,j) , rec(i+1,j-wv[i].first) + wv[i].second);
    return res;
}

void solve(){
    ios::sync_with_stdio(false);
    cin >> N;
    for(int i=0 ; i <N ; i++) cin >> wv[i].first >> wv[i].second;
    cin >> W;
    cout << rec(0,W) << endl;
}


int main(){
    solve();
    return 0;
}

记忆搜索

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e4;
/* 01背包问题 */
pair<int,int> wv[maxn];
int N; // 物品数量
int W; // 背包重量

int dp[maxn][maxn]; //2.多了个记忆数组(称为DP数组)

int rec(int i,int j){
    if ( dp[i][j] > 0 ) return dp[i][j];
    // 如果已经计算过,就直接使用之前的结果
    int res = 0;
    if( i == N) res= 0;
    else if( j < wv[i].first )
        res = rec(i+1,j);
    else res = max(rec(i+1,j) , rec(i+1,j-wv[i].first) + wv[i].second);
    dp[i][j] =res;	// 2.将结果记录
    return res;
}

void solve(){
    ios::sync_with_stdio(false);
    cin >> N;
    for(int i=0 ; i <N ; i++) cin >> wv[i].first >> wv[i].second;
    cin >> W;
    cout << rec(0,W) << endl;
}


int main(){
    solve();
    return 0;
}

动态规划解法

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e4;
/* 01背包问题 */
pair<int,int> wv[maxn];
int N; // 物品数量
int W; // 背包重量

int dp[maxn][maxn]; //2.多了个记忆数组(称为DP数组)

// 逆序推导
void solve(){
    ios::sync_with_stdio(false);
    cin >> N;
    for(int i=0 ; i <N ; i++) cin >> wv[i].first >> wv[i].second;
    cin >> W;
        for( int i= N-1 ; i >= 0 ; i--){
        for( int j=0;j<= W ; j++){
            if( j < wv[i].first ) dp[i][j] = dp[i+1][j];
            else
            dp[i][j] = max( dp[i+1][j] , dp[i+1][j - wv[i].first] + wv[i].second);
        }
    }
    cout << dp[0][W] <<endl;
}


// 顺序推导
void solve(){
    ios::sync_with_stdio(false);
    cin >> N;
    for(int i=0 ; i <N ; i++) cin >> wv[i].first >> wv[i].second;
    cin >> W;

    for( int i= 0 ; i < N ; i++){
        for( int j=0;j<= W ; j++){
            if( j < wv[i].first ) dp[i+1][j] = dp[i][j];
            else
            dp[i+1][j] = max( dp[i][j] , dp[i][j - wv[i].first] + wv[i].second);
        // 推导式也变了,下一行的依据上一行写成dp[i+1][j] = ...
        }
    }
    cout << dp[N][W] <<endl;
    // 输出的结果变了
}

int main(){
    solve();
    return 0;
}

▲注意，边界一定要注意处理。 这题由于边界全为0，而全局数组初始化默认是0，所以不需要处理，否则得像

国王和金矿提供的题解一样书写。

最长公共子序列问题

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e4;
/* LCS */
int dp[maxn+1][maxn+1];
void solve(){
    int m,n;
    cin >> n >> m;
    string sn,sm;
    cin >> sn >> sm;
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            if( sn[i] == sm[j] ) dp[i+1][j+1] = dp[i][j] + 1;
         // p[i+1][j+1] = max(dp[i][j] + 1 , max(dp[i+1][j] , dp[i][j+1]));化简而来
            
            else dp[i+1][j+1] = max(dp[i][j+1] , dp[i+1][j] );
        }
    }
    cout << dp[n][m] << endl;
}


int main(){
    solve();
    return 0;
}

完全背包问题

多重部分和