傅里叶变换->小波变化
声明:文中大多数内容来自(知乎1335)[https://www.zhihu.com/people/zhi-yuan-ya-77],matlab源代码:1368069096/From_FT_to_WT_examples-,部分为个人理解阐明
一.傅里叶变换FT
基础知识
(FOURIER TRANSFORM,简称FT)
为什么傅里叶变换可以把一个信号从时域变换到频域?
先给出公式,傅里叶变换的形式为:
PS:傅里叶变换还存在系数,有的文章写的是 ,有的文章写的是 ,两个系数只要满足正变换系数乘上逆变换系数等于 即可。这是为了保证经过一次正变换和反变换之后,得到的信号与原信号幅值相同,与我们接下来的讨论关系不大。
1.理解变换公式
我们知道,根据欧拉公式,。也就是说,傅里叶变换的本质就是:将原始信号乘上一组三角函数(正余弦),之后在整个时间域上积分。就这么简单!
y=sin(3t)图
我们来看一个信号:y = sin(3t),如下图:
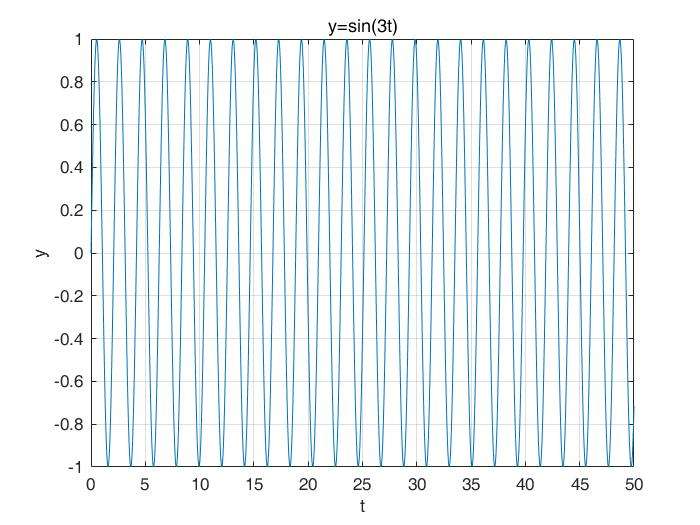
很好的周期性质,且每个周期的积分值都是0。如果对这个函数在积分,那就是基本是0,因为 包含了无数个周期。
PS:虽然这个积分在高数上不可积,但是你应该明白这里我要表达的意思:因为良好的周期性,且每个周期积分值是0,那么最后在很长的一段时间区间上积分,得到的还是一个很小的数,近似为0。
我们来用一段较长的时间区间计算一下,,结果符合我们的预计。
y=sin(4t)sin(3t)图
现在,我们来将这个信号乘上一个sin(4t) ,则信号变为y1 = sin(3t)*sin(4t),如下图:
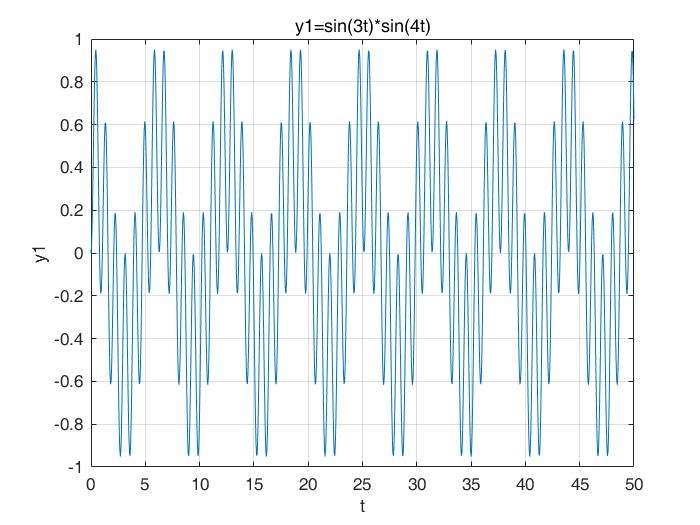
具有一个较短的小幅震动的周期和一个较长的主体周期,对吧?且每个主体周期的积分值都是0。同以上讨论,如果对这个函数在积分,基本还接近于0,因为 包含了无数个主体周期。
y=sin(3.1t)sin(3t)图
之后呢,我们来将这个信号乘上一个sin(3.1t) ,则信号变为y2 = sin(3t)*sin(3.1t),如下图:
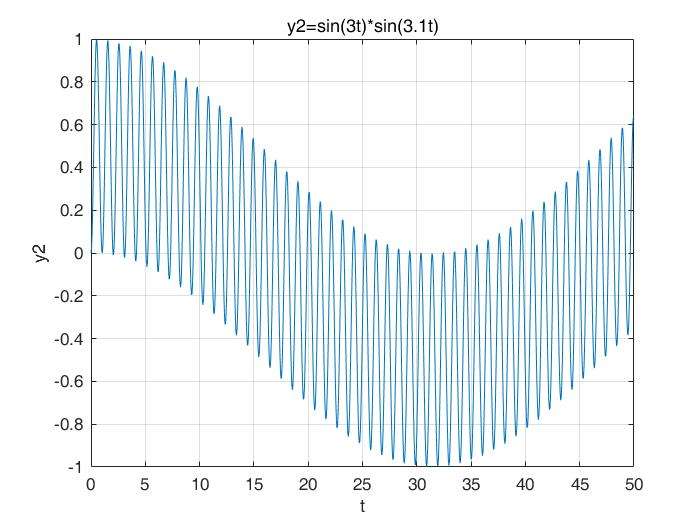
同样是有一个较短的小幅震动的周期和一个较长的主体周期,对吧?可以判断,每个主体周期的积分值都是0(虽然(0,50)这个区间没有完整地展示主题周期)。那么,依然同以上讨论,如果对这个函数在 积分,基本还接近于0,因为包含了无数个主体周期。
我们来用之前的时间区间计算一下, 。
咦?这一次怎么距离0这么远了呢?
原因就是:对于sin(3t)*sin(4t),它的主体周期较短,(0,50)是包含了好几个主体周期的,也就是说(0,50)在某种程度上是类似于 的。但是,对于sin(3t)*sin(3.1t),它的主体周期很长,(0,50)连它的一个完整的主体周期都没有包含,那么(0,50)是不能类似于 的,积分值自然就比较大。
我们此时可以这样小小总结一下,对于信号y = sin(3t),它的频率是3rad/s,(如果你喜欢用HZ,那就除以 ,就是 HZ,这里使用rad/s,是为了与前面的傅里叶变换的公式中的w一致),而sin(4t)的频率是4rad/s,sin(3.1t)的频率是3.1rad/s。
如果在 积分,那么y1 = sin(3t)*sin(4t),y2 = sin(3t)*sin(3.1t)的积分值都是0,也就是说,sin(4t)和sin(3.1t)在这里是没差别的。
但是!!!如果在一个有限区间内积分,由于sin(3.1t)的频率3.1rad/s,距离原信号y = sin(3t)的频率3rad/s更近,那么sin(3.1t)和sin(3t)的乘积,也就是y2 = sin(3t)*sin(3.1t)的积分的绝对值会更大,也就是会离0更远。这里已经显示出一定的频率选择性了。
最后,让我们请出我们今天的主角,将这个信号乘上一个自己同频率的sin(3t) ,则信号变为y3 = sin(3t)*sin(3t),如图:
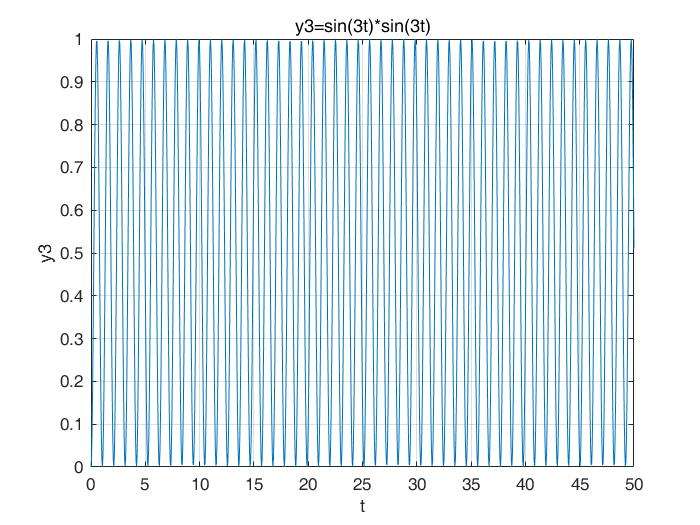
Amazing!!!发现了什么?良好的周期性?还有呢?**由于乘上了自己,任何时间的幅值都大于等于0了!不再满足周期内积分值为0这个条件了!**那么,此时,我们对这个信号在 积分,就会得到一个非常非常大的数字。这个很大很大的数字就告诉你,这个信号和你乘的信号是同频率的!这就是可以知道信号中具有哪些频率部分了,不是吗?
我们还是来用之前的时间区间计算一下, 。是不是比其他的积分值都大了好多?
好了,我们已经知道,▲.将一个信号乘上一个特定频率的sin函数,在 上积分,可以将信号中与sin函数同频率的部分筛选出来。那么,原则上讲,只要乘上所有频率的sin函数,并积分,不就知道原始信号中的所有频率部分了吗?
**但是这样做需要把所有频率乘进去,做无数次计算哈!**算不出来的。所以,我们将所乘的sin函数的频率作为符号变量w,来进行积分,即:
注意:这里的w只是一个符号变量,这样的话,就只需要做一次积分,可以计算了。
计算出来X(w)之后,想知道特定的频率w0对应的积分值,直接将w0带入X(w)就立马得到积分值。,如想知道是否含有w0=3rad/s分量,那么久计算X(3)看结果是否为0,这样就能知道原信号中是否含有这一频率的部分了。
好了,我们推导的这个式子,是不是与傅里叶变换的式子:
很像了呢?
这就是傅里叶变换的原理!乘上带有符号变量的sin、cos函数,并积分,就知道原始信号中的所有频率部分啦!
2、傅里叶变换(FT)的正交性
傅里叶变换是一种变换。在变换中,我们将原始信号乘上的变化信号称为基函数。
在傅里叶变换中,一系列不同频率的sin、cos等函数称为这个变换的基函数。至于为什么需要既使用sin,又使用cos,这涉及到一点点正交函数的概念。傅里叶变换中的不同频率的sin、cos等函数是正交函数,使用正交函数组成的基函数会带给变换一些方便。
什么是正交性?
向量正交:
我们都知道,向量的内积为。正交的定义为内积为0,即。如 表示x轴,$b=(0,1) $表示y轴,则 即意味着x轴与y轴正交。
假设有一个向量 , 在x轴上定位v, 在y轴上定位v。当x轴与y轴正交时,意味着x坐标和y坐标表示的信息是彼此独立的,两坐标可以完全定位v。
那么,当我们已知向量v,已知x轴a与y轴b,如果知道v的坐标呢?答案就是,投影/内积。
将v向x轴a做投影/内积: ,可以得到;将v向y轴b做投影/内积:,可以得到。
正交基
类似的,函数$ f_{1}(x), f_{2}(x) \int_{-\infty}^{+\infty} f_{1}(x) f_{2}(x) d x$。函数正交的定义同样为内积为0,即 。PS:对于周期函数,定义中的积分区间为一个周期T。
我们来看,
▲.因此,傅里叶变换中的不同频率的sin、cos等函数都是正交函数。我们将cos想象为一个轴,将sin想象为一个轴 ,这两个轴,就张了一个函数空间。
我们已经知道,x(t)的傅里叶变换为:
我们来看,实部 即相当于将x(t)与cos做内积,即向cos轴投影,得到的是在这个函数空间内的cos坐标,也就是与cos的相似度;虚部 即相当于将x(t)与sin做内积,即向sin轴投影,得到的是在这个函数空间内的sin坐标,也就是与sin的相似度。cos坐标和sin坐标都确定后,该信号就确定了。
因此,傅里叶变换之后,实部是与cos的相似度,虚部是与sin的相似度,傅里叶变换也就是与cos的相似度和与sin的相似度的总和,也就表示了相应的频率信息。
相似度的理解:通过相似度,可以将跟本身频率相似的频率挑选出来
3、小例子
最后,我们对于y=sin(3t)做傅里叶变换(这里画图用的matlab的FFT,是FT的离散快速算法,不是积分出来的,但是原理是相同的,仅做展示使用),变换后的图像如下:
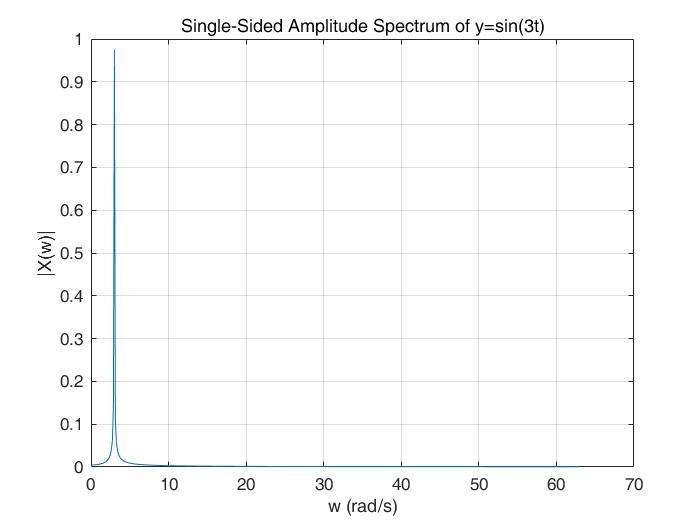
可以看到,与我们的预期相同,变换之后,在 处,出现了峰值,即表示该信号中包含了 的 频率成分。
这里需要说明三点:
1、这边的作图结果不是理想FT,如果是理想的FT,即在 上积分,那么除了 的积分值将是 之外,其他任意频率处的值都应该是0,得到的将是一个冲激函数。但是,这里我用的是离散傅里叶变换(详见我的下一篇文章),可以暂时理解为类似于我们讨论过的有限区间,当频率靠近3rad/s时(如之前提到的3.1rad/s的例子),也会积分出来一个较大的数值,所以这里不是一个冲击函数,而是一个山峰状的函数;
2、傅里叶变换之后是具有实部和虚部的,实部是与cos的相似度,虚部是与sin的相似度。我们要频率信息的时候,不管是与某一频率w的cos的相似还是与某一频率w的sin的相似,都是这一频率w嘛,不需要区分。因此,这里画图取了模,就不存在实部和虚部了。
3、在处之所以没有出现我们讨论的很大很大很大的值,是因为画图之前对于变换之后的幅值统一除以了信号取样点的个数,统一压缩了一定的倍数。
总结
1.由于sin和cos是一对正交基,所以所有的信号都可以分解成正弦信号与余弦信号的线性叠加。
2.除了与乘以本身频率w的正余弦相同信号再在范围上积分的结果会是非0以外,乘以其他频率信号的结果都是0.通过这个特性可以将是否含有w频率信号鉴别出
2.傅里叶变化的基函数由欧拉公式可分解为,所以根据公式:,前部分乘以cos(wt)能挑出cos成分中的信号频率,后部分乘以的sin(wt)能挑出sin成分中的信号频率。再将挑出的各信号频率线性叠加的结果就是分解信号总的含有各谐波分量的频率
二.傅里叶变换(FT)的缺点与短时傅里叶变换(STFT)
离散傅里叶变换(DFT)
在本文正式开始之前,我们需要明确一下实际信号进行的FT的一些特殊之处。实际采集的信号往往是这样的:
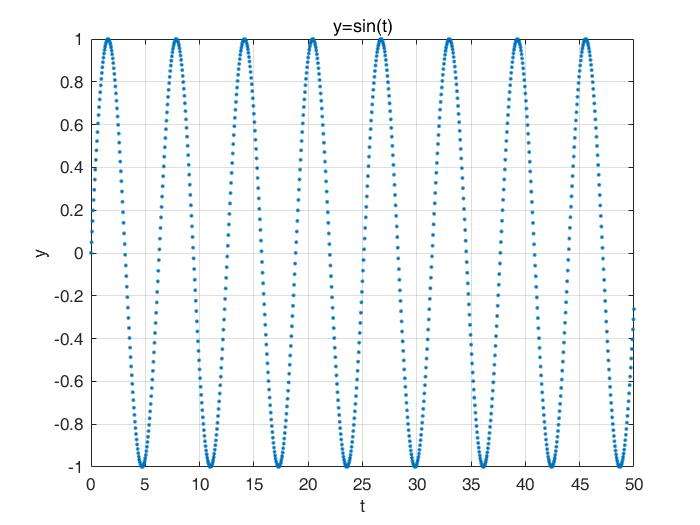
实际的信号往往具有两个特点:
1、离散性,就是采集数据不连续,很容易理解,采集信号肯定是一个一个数据采集的;
2、有限性,虽然理想的傅里叶变换是从 进行积分,但是实际信号往往实在一个区间内(a,b)的。
所以,我们要用到离散傅里叶变换(DISCRETE FOURIER TRANSFORM,简称DFT),DFT与FT相比,就是多了两个特征:1、离散型,2、有限性。
我们来一起试一试如何推导DFT公式。首先设采集了N个信号点,其时刻为 ,对应时刻采集到的信号值为 。很自然的,原来信号连续,是积分,现在数据离散了,那就是把积分变成累加。于是我们得到:
这么一来,我们发现,原信号有N个数据点,DFT变换后的信号却变成连续的了,我们将之称为离散时间傅里叶变换(DISCRETE TIME FOURIER TRANSFORM,简称DTFT)。
DTFT有两个缺点,第一, 且连续,需要进行无数次计算,计算机无法计算;第二,在进行计算的时候,我们需要已知:和 ,但是调用过FFT函数的同学都知道,FFT只需要已知就可以进行。
这是怎么回事呢?
首先,我们**使用相对采样时间 代替真实采样时间
,**可以得到:
。
此时我们发现, 变成了以 为周期的函数,即
那么,我们只需要计算 区间的 ,就可以得到 区间的了。也就是说,通过使用相对采样时间 代替真实采样时间,我们将
的范围从 缩小到了(0,).
自然地,我们希望将(0,)离散化称为N个点,这样计算机就可以计算了!则取,则有:
好了,这就是离散傅里叶变换DFT了!
接下来,来看DFT的两个性质:
-
第一,
,即
是所有元素的和,通常会比其他的元素大几个数量级。
-
第二,
,
,
,即第二个元素和最后一个元素共轭,同理有
等等。
如下图所示,DFT之后的N 个元素中,第一个为均值;之后的 N-1个元素,只有一半元素是独立的。
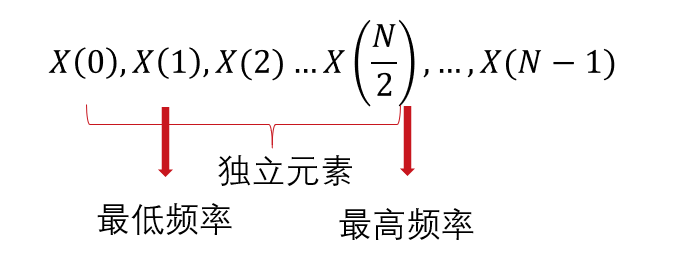
需要说明,这里 是一种相对频率,独立元素中,最小相对频域为1,最大相对频率为 。要想把
还原到真实的频率
,只需要
,将
映射到
即可,
为采样频率。
PS:简单说一下,根据香农采样定理,当采样频率为 时,能采到的最大信号频率为
。因此,将相对频率
通过公式
,得到的
就在区间
内,也就是真实频率的区间了。
所以DFT公式为:
PS:DFT公式的形式很多,有的是从时域到频域,有的是从空间域到频域,但是本质都是一样的,抓住离散性和有限性两个特点即可。离散性是指积分变成了累加,有限性是指积分/累加区间不是 了,而是一个有限区间了。
傅里叶变换(FT)的缺点
应该说明,虽然本小节的题目是FT的缺点,但是FT和DFT的本质是相同的。由于信号都是有限长度的、离散的,所以接下来进行的都是DFT,不过在某些部分为了方便理解,还是写了FT的公式。在看本文的时候,你不需要刻意区分这两个概念。
我们现在来看两个信号,如下图:
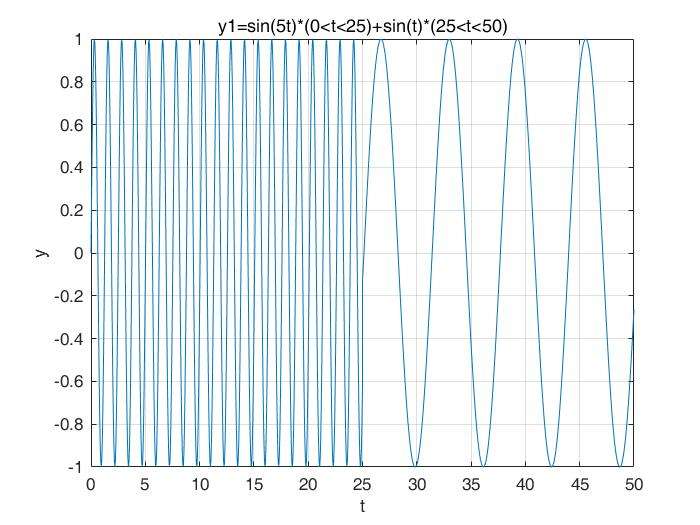
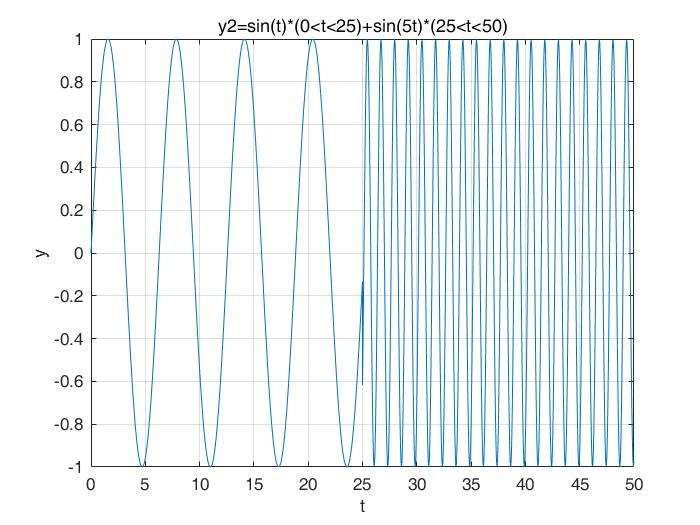
这两个信号都是由sin(t)和sin(5t)组成的,y1是先出现了sin(5t),再出现了sin(t),y2是先出现了sin(t),再出现了sin(5t)。
我们对它们进行FT,看看他们包含怎么样的频率,如下图:
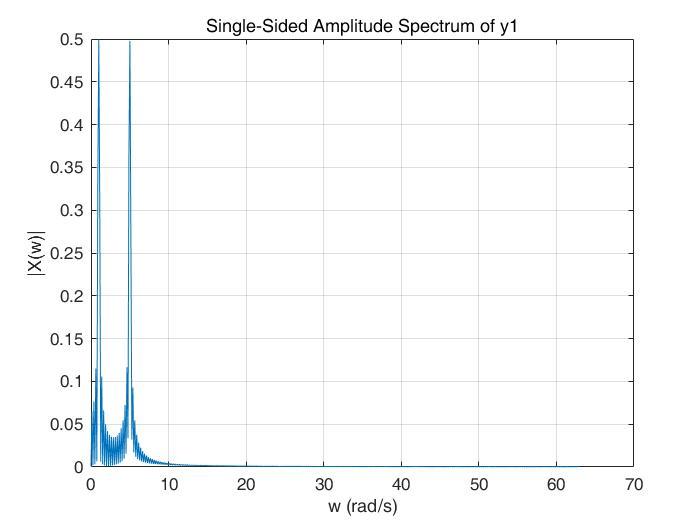 y1,FT
y1,FT
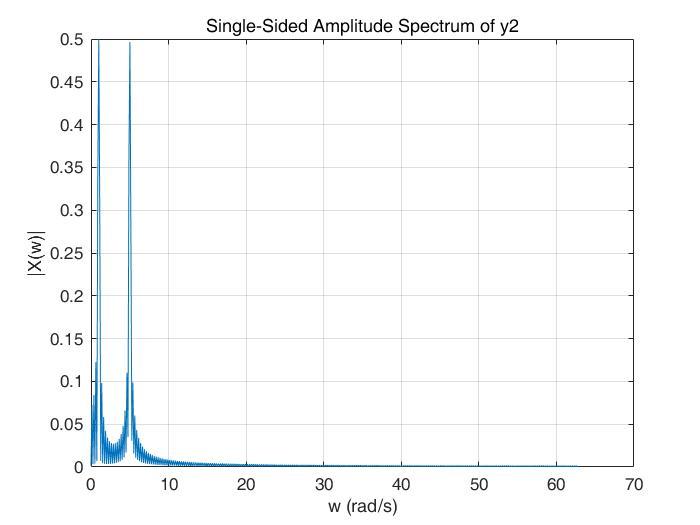 y2,FT
y2,FT
Amazing!发现了什么?变换后的结果是一模一样的,都在w=1rad/s和w=5rad/s出现了峰值!这就可以说明FT的缺点了——FT只能提供频域信息,而完全丢失了时域信息!!!
不管某一频率的信号出现的时间是早还是晚,FT都是将它一视同仁地乘上sin和cos(FT的变换基函数),然后在整个时间区间加和。因此,它不能提供某一频率信号出现的时间。
比如,对于上面两个信号,FT只能告诉我们,它们都有1rad/s和5rad/s的频率,而不能告诉我们1rad/s和5rad/s分别出现在哪个时间段。
所以,怎么办呢???
那就是把信号分成左右两半啊!左边进行一次FT,右边进行一次FT,很简单吧!好了,这就是短时傅里叶变换(STFT)的基本原理。
所以,接下来我们要正式开始步入——短时傅里叶变换(STFT),看看它是如何解决这个问题的。
短时傅里叶变换(STFT)
如上所述,我们将信号从中间截断,左边进行一次FT,右边进行一次FT,分别来看看。
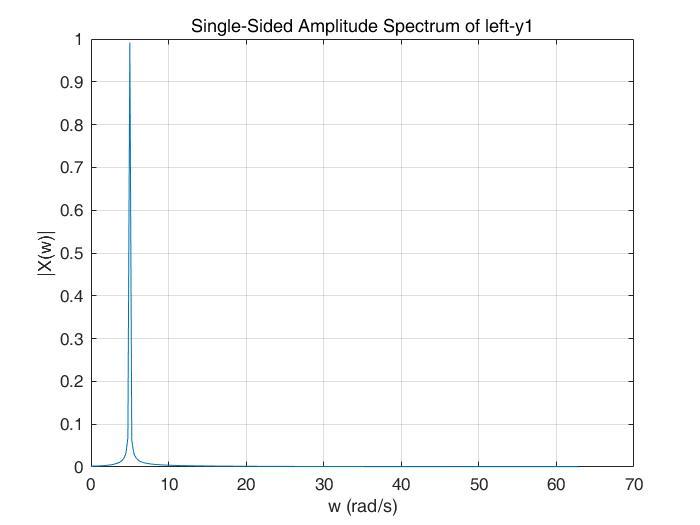 y1左
y1左
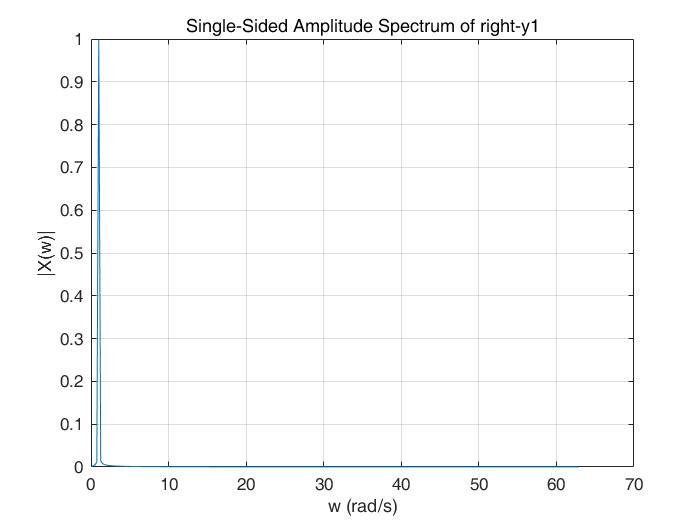 y1右
y1右
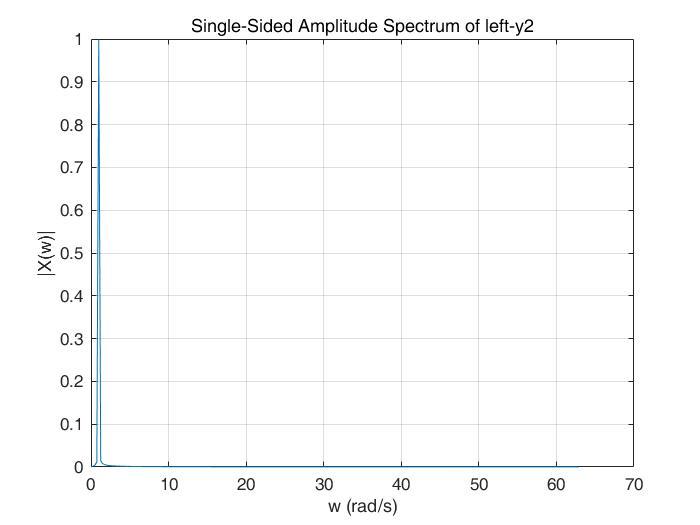 y2左
y2左
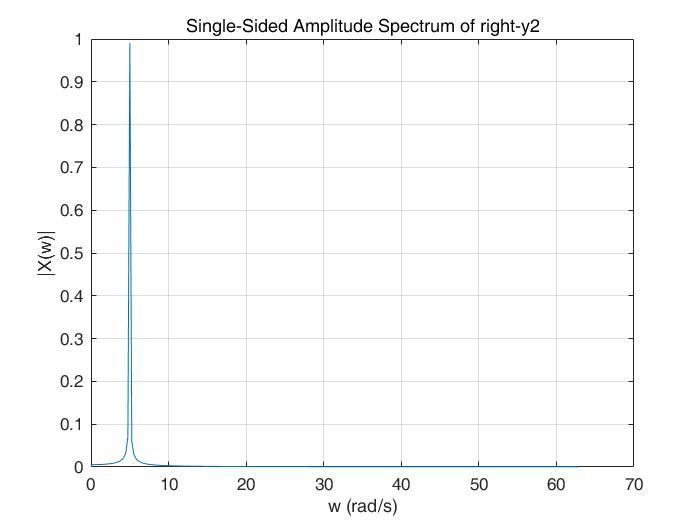 y2右
y2右
可以看出,y1的左半部分是5rad/s,右半部分是1rad/s,y2恰好相反。这就说明,在y1中,(0, 25)的信号是5rad/s的频率,(25, 50)的信号是5rad/s的频率,y2恰好相反。这就是短时傅里叶变换的基本原理。
但是数学嘛,能用一个公式表达的,就别用一段话表达,截断、切开这些语句太不专业了。截断、切开的操作,更专业的讲叫作分窗,其实是可以通过数学上的处理变成DFT变换的基函数的一部分的。接下来我们来看一看。
首先,你可以想象一下,有一个窗子在这个信号上从左向右滑动,每次你都只能看到这个信号的一部分,所以我们把这个长度叫作窗长width。
现在我们来定义一个方窗函数 ,如下图,即是width = 10 的一个方窗函数:
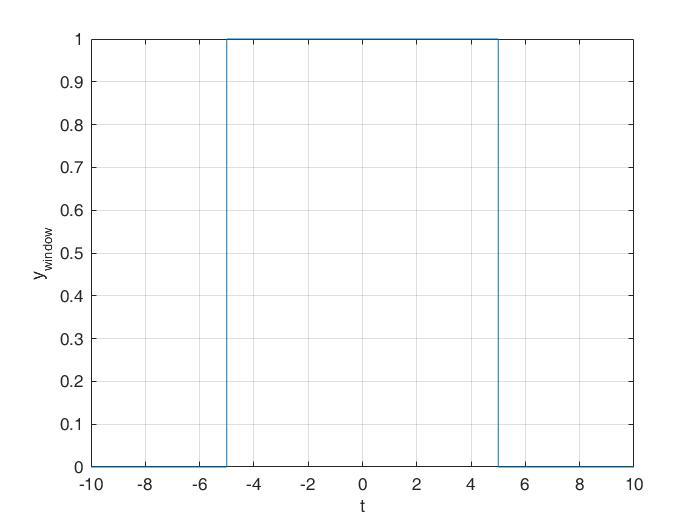
定义了方窗函数之后,我们只需要对方窗函数进行平移,再与原信号作乘,就相当于原来的截断、切开的操作,因此这种操作更专业地叫作分窗。
那么,将方窗函数向右平移了 (s可能是sliding的意思吧),再与原信号相乘,由于方窗函数除了中心的width部分是1外,其他部分都是0,这就相当于提取出了原信号在
处,宽度为width的部分,这个信号分窗这个操作就可以写成:
。
如下两图所示,将 与
相乘,就相当于取出来了
中的(20,30)中的一段。
那么,我们对原信号中被提取出来的这一部分进行FT,就可以写成:
PS:这里之所以 要变成
,是为了保证做FT的时候相乘的基函数具有统一性。
如此,变换后的代表原信号在
处、宽度为width的部分的傅里叶变换,也就可以提取出来原信号在
处、宽度为width的部分,包含各个频率部分的多少!带入不同的
,也就是随着窗子的滑动,就可以知道不同的时间段内频率的成分。
我们采用width为10的方窗函数对进行STFT,如下:
首先,方窗函数位于 处,与原始信号相乘,选择出(0,10)的信号。
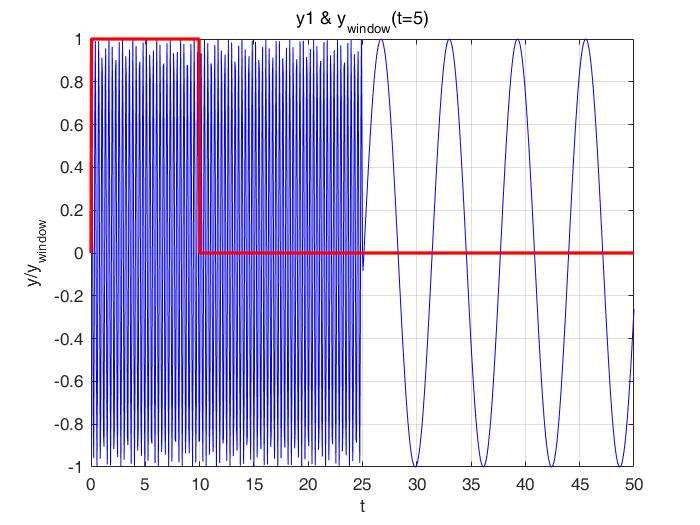
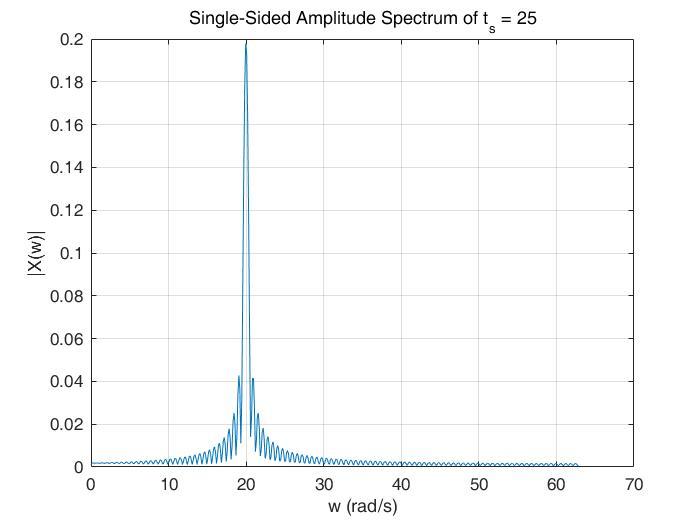
对选择出来的信号进行FT。可以看到,当t=5s时,选择的时间区间为(0,10),这一部分只包含了 的频率成分。
之后,方窗函数向右移动,与原始信号相乘,选择出不同时间区间的信号,进行FT。这里选择t=25s进行展示。
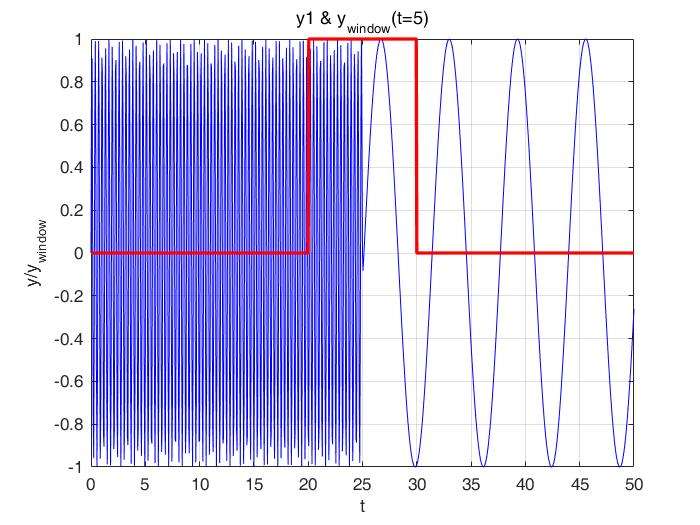
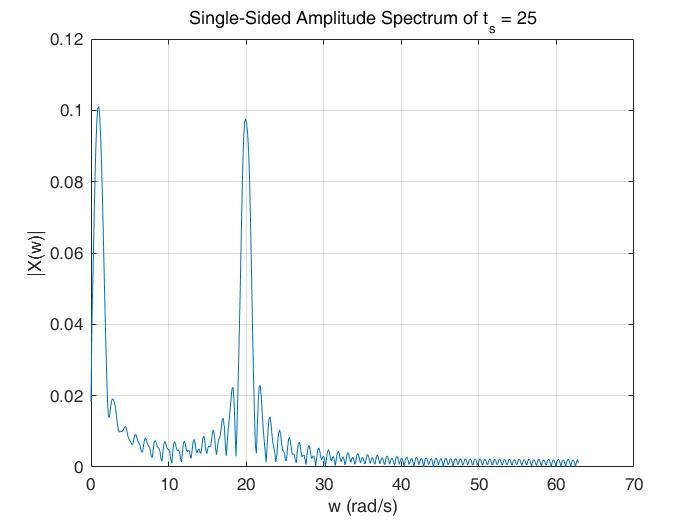
可以看到,当t=25s时,选择的时间区间为(20,30),这一部分即包含了 的频率成分,也包含了
的频率成分。
重复以上过程,我们可以将方窗函数选择的不同时间区间的信号的FT的结果拼合起来,形成一张三维图。由此,我们即可知道,在 的时间区间内,信号具有怎么样的频率成分。
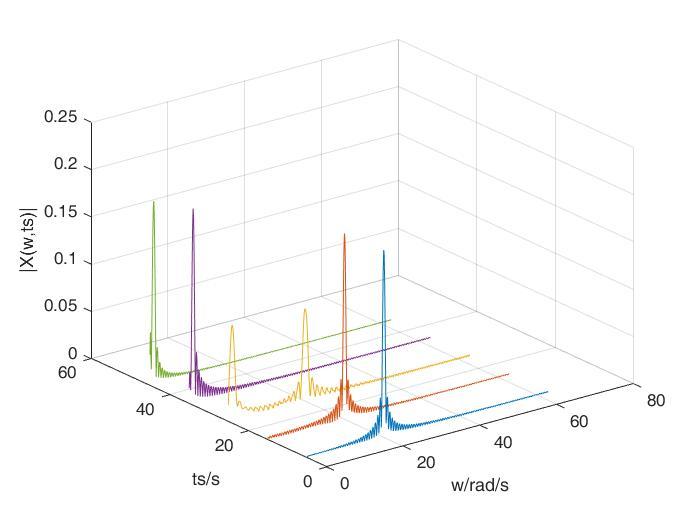
通过width = 10的方窗的STFT结果,我们可以知道,对于信号: ,在(0,10)、(10,20)时间区间内,具有20rad/s的频率成分;在(20,30)时间区间内,具有1rad/s和20rad/s的频率成分;在(30,40)、(40,50)时间区间内,具有1rad/s的频率成分。
最后,进行三点重要的讨论。
第一点,变换之后的 是一个三维函数,它有两个自变量,
和w。
指的是原信号在
**处,**w上一篇文章我们已经讨论过了,就是频率。所以,STFT提取出来的信息就是:原信号在
处、宽度为width的部分,包含的频率信息。
原则上讲,可以得到任一对应的频率成分,如下图。
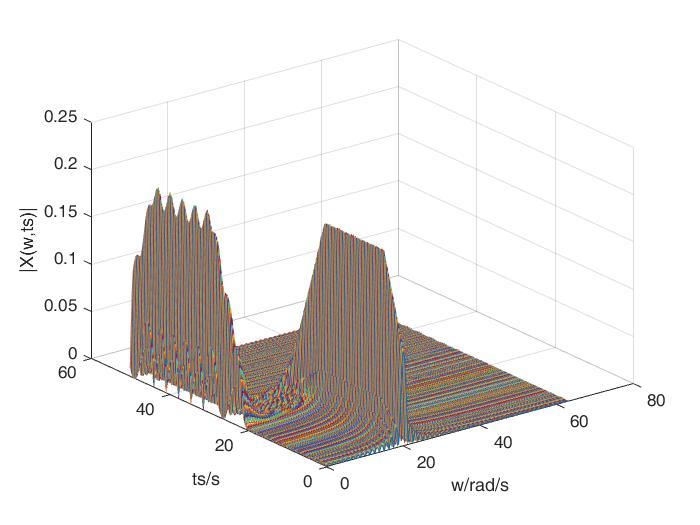
但是 是连续的,并不意味着你知道了每个时刻的频率成分,你知道的还只是
这一段区间内的频率信息。所以一般不需要计算所有的
,每隔width计算一次即可。
你或许会想,我**把width缩小一些,不就可以知道更精确的时间范围内的频率了吗?**是的,你的猜想很对!但是,**如此做也会带来一些频域分辨率的问题。**这一点涉及到一些时域分辨率和频域分辨率的知识,我们下一篇文章会着重讲。
本质变化:
第二点,方窗函数是可以包含入变换基函数内部的,这组成了新的基函数,同时反映了STFT的本质。
我们来看, 如果定义 ,那么
那么,STFT的公式: 就可以写成:
我们在上一篇文章里说过,变换就是将原信号乘上一个基函数,再积分的过程,那么,SDFT的基函数就是 !
Amazing!所以,STFT的本质是什么呢?
**STFT的本质就是将FT的基函数 乘上一个方窗函数,形成了一个新的基函数
!**前面说的分窗、截断之类的都是表象,STFT的本质是基函数的改变!
那么,为什么STFT的基函数可以用于分窗,而FT的基函数不行呢?我们来看,我用正弦函数sin(5t)表示原来的基函数 ,那么FT基函数和STFT基函数如下:
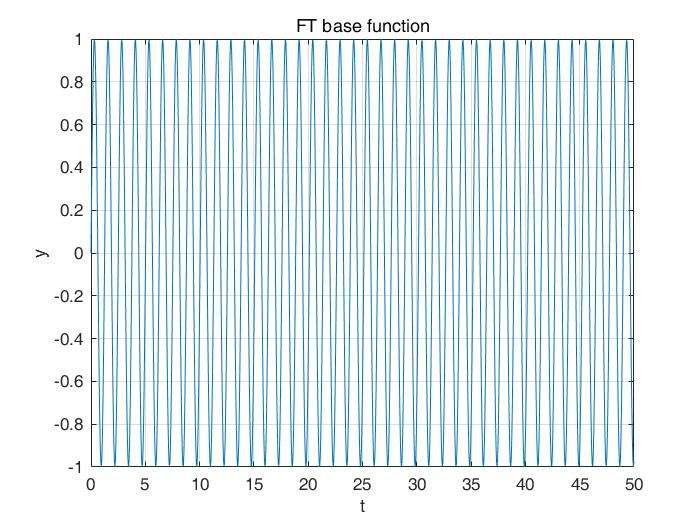
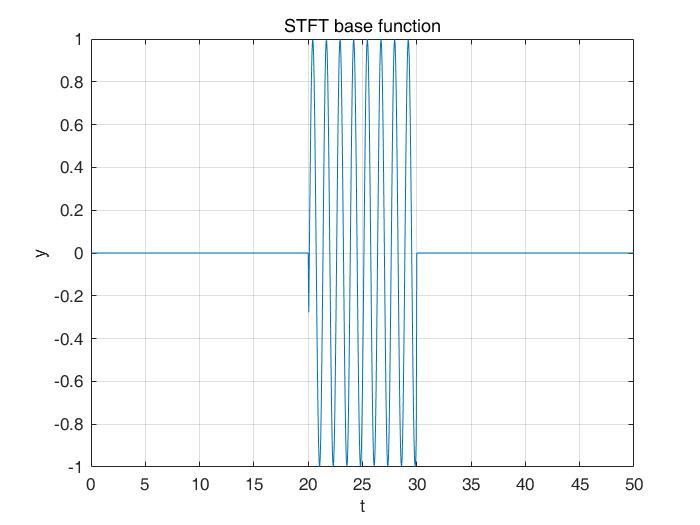
原因就是:FT的基函数是在时域无限延伸的,因此,无论怎么平移,都是任分布在整个时域的,起不到分窗的作用。而STFT的基函数只在时域一段不为0,在剩下的时域都是0,因此,STFT的基函数的平移,就相当于自动加了窗子啦!
紧支撑性:
这种只在时域一段不为0,在剩下的时域都是0的性质被称为“紧支撑性”(compactly supported),具有这种性质的函数,平移之后与一个信号相乘,就相当于分窗操作。这一点很重要,我们之后讲小波变换的基函数的时候还会讲。
第三点,我们前面对于分窗操作使用的函数一直称为“方窗函数”,这是一种最理想的窗函数。还有一些其他的窗函数,比如,汉宁窗、海明窗、高斯窗等。窗函数本质都是一个窗子而已,原理是一模一样的,上面所有的讨论也都成立,只是这些窗子会让信号稍稍变形一丢丢而已。你就想像方窗函数就是一面平面镜,其他的窗函数就是哈哈镜就行了。
总结:
Q:为什么要用相对采样时间代替真实采样时间?
A:原来做傅立叶变换,既需要知道真实采样时间,也需要知道采样数据,用相对采样时间替代真实采样时间之后,只需要知道采样数据。这极大地拓展了傅立叶变换的使用范围。比如,并不是所有傅立叶变换的对象都可以具有真实采样时间。一副图像也是可以傅立叶变换的,但是在图像里,并没有采样时间这个概念,只有0123456这些像素索引值,对图像做傅立叶变换,就是把索引值作为相对采样时间。
三.短时傅里叶变换(STFT)的缺点与连续小波变换(CWT)
三、短时傅里叶变换(STFT)的缺点与连续小波变换(CWT)
1、分辨率问题
首先,我们需要了解一下海德堡测不准原理: ,
为信号的时间不确定度,
为信号的频率不确定度。即,我们永远无法同时确定一个信号的确切时间和确切频率。
原因比较简单,频率其实就是时域周期性。如果我只给你一个数据点,问你这个数据点的频率是多少,这肯定是做不到的。要确定频率,就需要一个时域区间(包含几个时域周期)的信号。
时域区间越宽,信号的时间定位越不准,时间不确定度 越大,但是得到的频率越准,频率不确定度
越小;我们称之为:低的时域分辨率,高的频域分辨率。
时域区间越窄,信号的时间定位越准,时间不确定度 越小,但是得到的频率越不准,频率不确定度
越大;我们称之为:高的时域分辨率,低的频域分辨率。
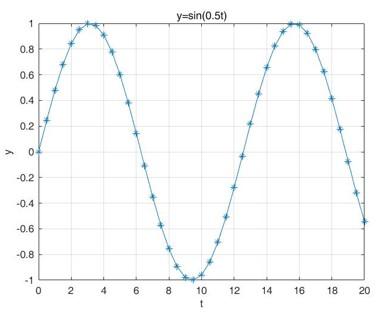
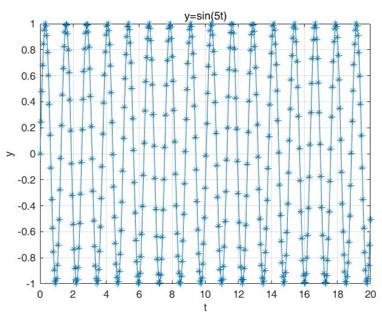
如上两图,对于第一个图中 的信号,要确定频率,即使把
都拿来,还是不太准,因为只包含了一个周期;对于第二个图中
的信号,要确定频率,取个
就差不多了,因为已经包含了好几个周期了。
我们来总结一下。
对于低频信号,为了更好地确定频率,我们希望,时域区间宽一些,即时间不确定度 大一些,根据海德堡测不准原理,频率不确定度
自然小一些;即低频信号,我们希望:宽窗子,低的时域分辨率,高的频域分辨率。
对于高频信号,为了更好地在时域定位,我们希望,时域区间窄一些,即时间不确定度 小一些,根据海德堡测不准原理,频率不确定度
自然大一些;即高频信号,我们希望:窄窗子,高的时域分辨率,低的频域分辨率。
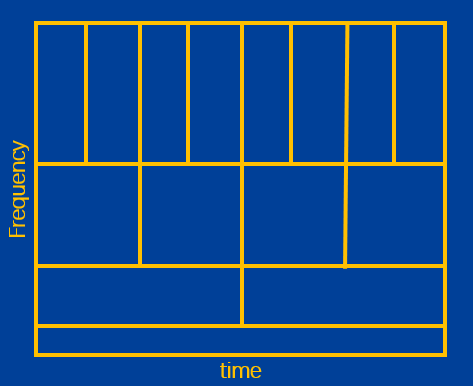
上图所示是我们希望的动态分辨率。图中每个小矩形的 轴方向的宽度是时间区间大小,
轴方向的宽度是频率区间大小。注意,每个小矩形的面积是相等的,这保证了时域分辨率乘上频域分辨率是定值,最大程度满足海德堡测不准原理。通过图可以看出,我们希望,对于低频信号:低的时域分辨率,高的频域分辨率;对于高频信号:高的时域分辨率,低的频域分辨率。
对于整体低频、局部高频的信号,这种动态调整分辨率的规则特别有用。在实际信号中,频率非常高的高频信号往往是一种噪声,只在局部出现,基本都满足整体低频、局部高频这一条件。
最后,我们再来看两张分辨率图来强化一下对于分辨率的理解。
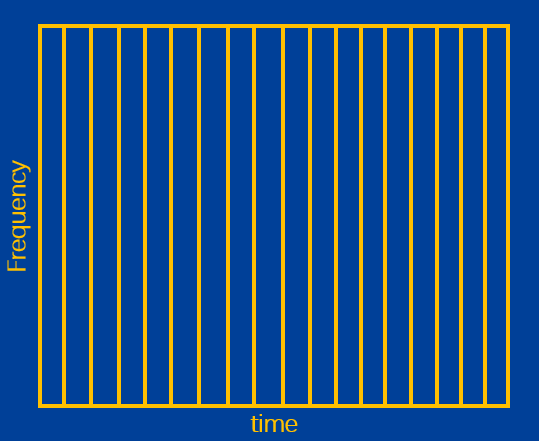
上图是一张采集信号的分辨率图。每个小矩形的 轴方向的宽度是很小,
轴方向的宽度很大。也就是说,其时域分辨率很好,可以确切地确定每个信号采样点的时间,但是其频域分辨率很差,或者说完全不具有频域分辨率。

上图是一张傅里叶变换(FT)的分辨率图。每个小矩形的 轴方向的宽度是很大,
轴方向的宽度很小。也就是说,其频域分辨率很好,可以比较精确地确定信号中的频率成分,但是其时域分辨率很差,或者说完全丢失了时域分辨率。
傅里叶变换的这一特性,这一点我在上一篇文章里讲过,这也是我们转而使用短时傅里叶变换(STFT)的原因。
2、短时傅里叶变换(STFT)的缺点
我们来回忆一下STFT(详见:1335:从傅里叶变换进阶到小波变换(二)),STFT的窗长是固定的,即时域分辨率是固定的,根据海德堡测不准原理,其频域分辨率也是固定的。其分辨率图如下:
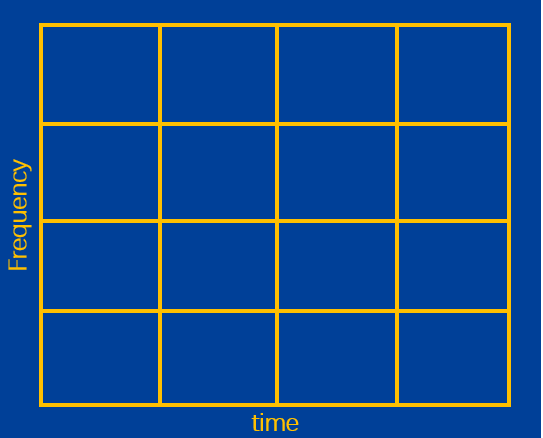
每个小矩形的 轴方向的宽度和
轴方向的宽度是恒定的!也就是说,不论高频低频,其时域和频域分辨率都不可调,这与我们之前讨论的“对于低频信号:低的时域分辨率,高的频域分辨率;对于高频信号:高的时域分辨率,低的频域分辨率”这一原则不符合。
这种不符合会带来什么后果呢?
如图所示正弦信号,0250ms:300HZ,250500ms:200HZ ,500~750ms:100HZ , 750~1000ms:50HZ。
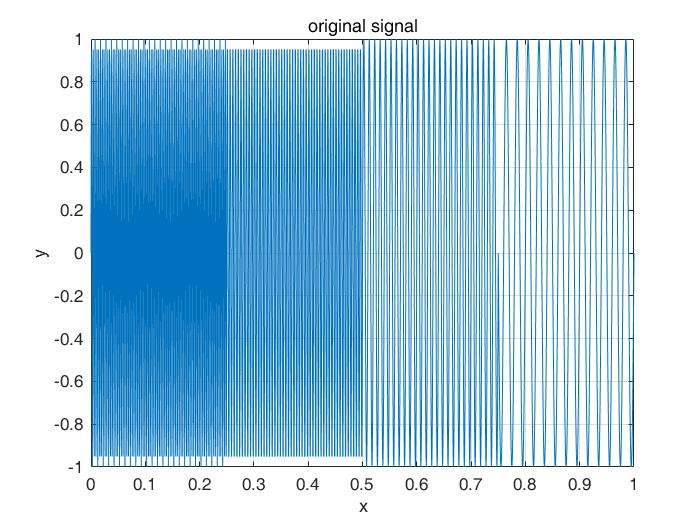 )
)
选择一个较窄的窗子 做STFT,结果如下:
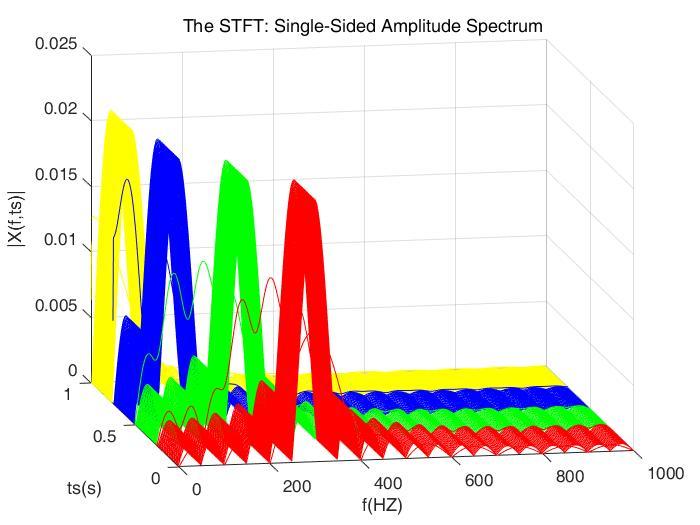
当窗子较窄的时候,STFT的时域分辨率还行,但是频域分辨率不佳。
我们选择一个宽一些的窗子 做STFT,结果如下:
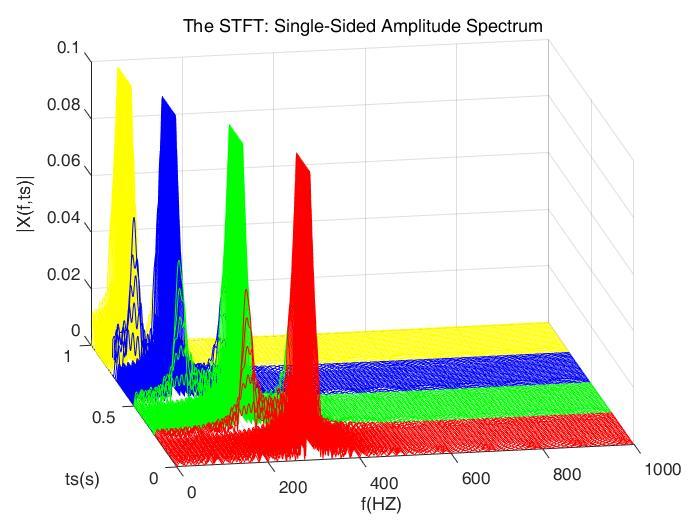
当窗子较宽的时候,STFT的频域分辨率很好,基本可以确定频率,但是时间轴上开始出现交叠了,也就是时域分辨率下降了。
我们选择一个更宽的窗子 做STFT,结果如下:
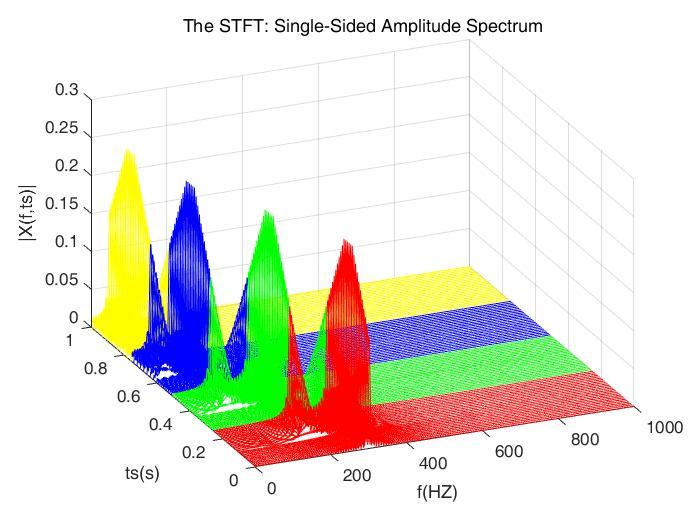
当窗子更宽的时候,STFT的频域分辨率非常好了,但是时域分辨率已经很差了,时间轴上出现了大规模的交叠现象。
我们来总结一下,对于STFT,如果窗子的宽度选择合适,是可以得到时域和频域分辨率都“还可以”的结果的(由于STFT的分辨率固定,只能说“还可以”,不能说“满意”,因为我们最想要的是动态分辨率)。但是,在变换之前,我们也不知道选择多宽的窗子是合适的。
这就是STFT的缺点:1、时间和频率分辨率都固定,不能随着频率的高低实现动态可调;2、选择一个合适的窗宽十分困难。
3、连续小波变换(CWT)
为了实现动态分辨率,我们引入了小波母函数。
需要说明,小波母函数并不是一个特定的函数,而是一种函数的集合,满足了一定条件的函数均可以作为小波母函数。小波母函数 需要满足的有:
条件1,紧支撑性: ,即仅在一小部分定义域里不为0,剩下部分均为0。这个性质带来的便利我们在前一篇文章讲过了,就是具有紧支撑性的基函数,在原信号的时间轴上平移,就相当于对于原信号就行了加窗操作。
条件2,波动性: ,即在所有定义域内积分值为0,这说明小波母函数是一个波。
条件3,容许条件: ,这个条件使变换可逆。其中,
是小波函数傅里叶变换的共轭。由3可知
,也就是条件2。
条件4,正交性:这个条件也是为了使变换可逆。
PS:条件3、4的数学证明比较复杂,所以仅仅提了一下他们的作用,就是使得变换可逆。
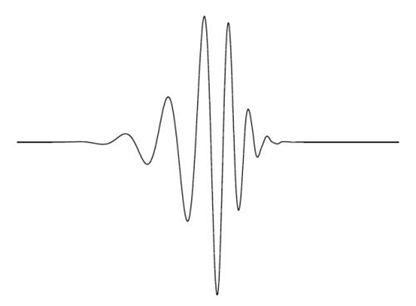
上图就是一个小波母函数的例子,我们看到了:
1、紧支撑性:仅在一小部分定义域里不为0,剩下部分均为0;2、波动性: 在所有定义域内积分值为0。这两个条件是满足的。
小波母函数既然是一个波,那么就具有频率。根据我们第一篇文章讲的内容(1335:从傅里叶变换进阶到小波变换(一)),将小波母函数作为基函数,与采集到的信号相乘并积分,可以筛选出:信号在小波母函数非0部分,频率与小波母函数相近的成分。
需要说明,不同于FT的基函数 ,小波母函数不具有特定的某一频率,而是具有一个范围内的频率,因此筛选的是一定范围的频率,类似于一个带通滤波器。
接下来我们讲一讲,小波母函数的变换,变换公式如下:
一是平移,用上式中的 控制,
改变,就相当于
在时间轴上不断的平移。
二是缩放,用上式中的 控制。
变换后的函数 称为小波函数。
如下图,中间的图, 较小,相当于挤压;右侧的图, **较大,相当于拉伸。**变换公式前的是为了能量守恒,没有特别目的。
。下图中蓝色部分为小波函数(但原图没画成波的形式,只是表示小波函数的时间轴位置和不为0的部分的宽度),黄色部分为信号。
,用来筛选高频部分。小波函数在时间轴上平移,每一次平移就先相乘,再积分,筛选出信号中与自己频率相近的部分。
此时,窗子较窄(小波函数不为0的部分窄),时间分辨率好,频率分辨率差。
,用来筛选中频部分。小波函数在时间轴上平移,每一次平移就先相乘,再积分,筛选出信号中与自己频率相近的部分。
此时,窗子变宽了(小波函数不为0的部分变宽),时间分辨率变差,频率分辨率变好。
,用来筛选低频部分。小波函数在时间轴上平移,每一次平移就先相乘,再积分,筛选出信号中与自己频率相近的部分。
此时,窗子很宽(小波函数不为0的部分很宽),时间分辨率差,频率分辨率很好。
这就是连续小波变换CWT啦!
将上述CWT的过程写成公式就是:
注意:上图中我们只列举了三种 (即三次缩放)和4种 (每种缩放对应四个时间位置,但是事实上,
是连续的,无穷多个的。
还是这个正弦信号,0250ms:300HZ,250500ms:200HZ ,500~750ms:100HZ , 750~1000ms:50HZ。
:
。
这也就再一次说明了CWT是动态分辨率的,这也是CWT相对于STFT的优势所在。
4、FT、STFT、CWT基函数对比
最后,再来看看,FT、STFT、CWT的基函数之间的不同,以便加深理解。
,具有了紧支撑性,时域平移等同于分窗,使得STFT既能筛选频率,也能筛选时间。但是STFT基函数是:先确定频率,再与窗函数相乘构成的。因此不同的频率,具有同样的时间和频率分辨率。另外,窗函数的长短也比较难以确定。
CWT的基函数,是小波函数,具有紧支撑性,时域平移等同于分窗,使得CWT既能筛选频率,也能筛选时间。小波函数在改变频率的时候,是通过**“缩放”**实现的,**这使得小波函数在改变频率的同时,改变了窗长。**因此不同的频率,具有不同的时间和频率分辨率,实现了分辨率动态可调。
最后,再说一下,有很多类型的小波母函数,比如haar小波,db系列小波,sym系列小波,coif系列小波等等等等。具体哪一个小波适应哪种情况,估计都能写一本书了,我也没深入钻研过。我在利用小波变换做肌电信号识别的时候就是读一读有关肌电信号识别的论文,看看别人试过哪些小波,是一种上手比较快的方法。
连续小波变换(CWT)的缺点与离散小波变换(DWT)
四、连续小波变换(CWT)的缺点与离散小波变换(DWT)
1、连续小波变换(CWT)的缺点
在上一篇文章(https://zhuanlan.zhihu.com/p/68323379)中我们讲解了 CWT可以实现动态分辨率的时频分析。CWT公式为:,
表示原始信号。你可能已经注意到了,这里的
是一个连续函数。
但是在第二篇文章(https://zhuanlan.zhihu.com/p/66246381)中我们讲过,实际采样信号往往具有两个特点:1、离散性,就是采集数据不连续,很容易理解,采集信号肯定是一个一个数据采集的;2、有限性,虽然理想的CWT是从 进行积分的,但是实际信号往往实在一个区间内
的。如下图所示。
所以,由于CWT需要一个连续信号,但是实际采样信号往往是离散的,我们无法直接对实际信号进行CWT。
或许你想,我们对实际采样信号进行插值连续化不就可以使得其连续了吗?
是的。将实际采样信号插值连续化之后,我们——人,是可对它进行CWT的。
但是,我们也都知道,我们的帮手——计算机,是无法处理连续问题的。计算机只能处理离散问题。如果计算机要进行CWT,就意味着需要计算机做无穷次运算,计算机计算能力再强也是做不到的。
因此,为了使得计算机可以进行小波变换,我们需要引入离散小波变换(DWT)。
2、离散小波变换(DWT)的Wallet算法
DWT有很多种实现方式,我们在这里介绍Wallet算法,它是DWT的以一种经典的快速算法,也比较易懂。
我们首先来回顾一下上一篇文章讲过的动态分辨率图:高频部分,窄窗,高的时域分辨率,低的频域分辨率;低频部分,宽窗,低的时域分辨率,高的频域分辨率。
我们是利用小波母函数的挤压和拉伸来实现动态分辨率的:
当小波母函数被挤压的时候,频率就高,此时窗子窄,时域分辨率就好,根据海森堡测不准原理,频域分辨率就差;
当小波母函数被拉伸的时候,频率就低,此时窗子宽,时域分辨率就差,根据海森堡测不准原理,频域分辨率就好。
也就是说,我们控制的是不同频率对应的窗长(即时域分辨率),频率分辨率是通过海森堡测不准原理得到的,从而达到了动态分辨率。
那么,如果我们这次不控制窗长(即时域分辨率),转而控制频域分辨率,能否达到动态分辨率呢?
答案是可以,这就是Wallet算法要解决的问题。
半子带滤波
我们知道,小波母函数本质上是一种带通滤波器。那么,假设可以通过小波母函数构造得到两个滤波器(至于怎么得到后续会介绍一下),包括一个高通滤波器和一个低通滤波器。
假设信号中的最高频率为 。那么,高通滤波器的作用就是得到
的部分,低通滤波器的作用就是得到
的部分。如下图所示:
我们将这个过程称为一次半子带滤波。
下采样与上采样
我们定义一个N倍下采样过程:将采样点N倍稀释。如下,就是一个2倍下采样过程,将采样点稀释2倍,即:每2个点采样数据点,就去除一个点。
N倍上采样过程:将采样点数量增加N倍。一般通过补0,或者插值的方法实现上采样。
离散小波分解
我们将一次半子带滤波+一次2倍下采样称为一层小波分解。如下图所示,图中的“箭头+2”表示一次2倍下采样。
假设原采样信号有 N 个点,信号最高频率为 (根据采样定律,
为采样频率的一半)。
经过一次高通滤波后,得到了 的部分,也是 N 个点,再经过一次2倍下采样,变成了 个点,我们将这个点称为小波分解的高频系数(为什么叫作系数会在后面解释)。
经过一次低通滤波后,得到了 的部分,也是 N 个点,再经过一次2倍下采样,变成了 个点,我们将这个点称为小波分解的低频系数。
也就是说,经过一层小波分解的信号,它的总长度加起来,还是 N ,是不变的。
现在,我们已经对 个点的原信号进行了第一层小波分解,得到了
个点的高频系数和
个点的低频系数。
那么,我们保持 个点的高频系数不变,把
个点的低频系数作为信号,再进行一次小波分解。于是可以得到
个点的高频系数和
个点的低频系数。
这个过程被称为**第2层小波分解。**我们验证一下,经过2层小波分解的信号,它的总长度加起来,还是N ,是不变的。
依此类推,我们可以进行第三层,第四层小波分解,如图所示,直到第 层小波分解。在第
层小波分解,由于不断的下采样,低频系数和高频系数都只剩1个数了,小波分解无法进行下去了。
因此,小波分解的原始信号个数一般也需要是2的幂次。不过,在各种数学计算软件里,如果输入不是2的幂次,它会自动帮你补零到2的幂次。
我们取4层小波分解的结果来看一下。
在频域上,我们得到的是 ,
,
,
,
频域区间的系数。
在时域上,由于不断的2倍下采样,不断地丢弃数据,所以最后一层分解得到的,
的时域分辨率最差,第一层分解保留的
时域分辨率最好。
那么,我们得到的分辨率就是这样子的:
这,不就是上一篇文章我们讲过的小波变换得到的动态分辨率吗?
是的!这就是离散小波变换的快速算法之一——Wallet算法,通过不断的半子带滤波和下采样,控制不同频率成分的频域分辨率,进而达到动态分辨率。
最后,用一张比较经典的图,再来演示一下小波分解的过程。 为采样信号的最高频率。
代表高通滤波器,
代表低通滤波器,“箭头+2”表示2倍下采样。
图源:THE WAVELET TUTORIAL
再来举个例子形象地说明一下DWT的使用吧。
希望对于一个采样率为1000HZ的非稳态信号进行小波分解,下图为包含了256个采样点(即256ms)的原始采样信号。
1、首先,选择小波分解的层次。
可以根据对最低频率区间的要求来选择小波分解的层数。比如,我之前做项目的时候,采样率为1000HZ,那么信号的最高频率为 。我认为对于频率低于20HZ的成分,不需要再进一步区分了。因此,我选择5层小波分解,得到的最低一层的频率区间为
,即为
,这就够用了。
2、接下来,进行5层小波分解,得到小波分解系数。
如下图中,图1依然是原始采样信号 ,图2到图6为第1层到第5层小波分解的高频系数,图7为第5层小波分解的低频系数。如图所示,这些小波分解系数对应着不同的频率区间。
这就是DWT了,又称为小波分解。
这里提一下,小波分解是可逆的,即可以通过不同频率区间的小波分解系数进行重构,得到不同频率区间的重构信号。
3、所以,最后,进行小波重构,得到重构信号。
如下图中,图1依然是原始采样信号,图2到图7为通过不同频率区间的小波系数进行重构,得到的重构信号。将图2到图7加起来就可以得到重构原始信号,其和原始采样信号的误差称为重构误差。
3、Wallet算法背后的数学原理简介
这一部分主要是为了解答上一部分中的两个问题。
1、在上一部分,我们“假设可以通过小波母函数构造得到两个滤波器”,那么,怎么得到刚好可以具有以上特性的滤波器呢?
2、在上一部分,我们将小波分解之后的结果称为“系数”,那么,为什么称为系数呢?
先说一下,这部分我不是弄得非常懂,毕竟我只是个做工程的本科生,不是做数学的大佬。我凭自己的理解写一写大概,并推荐了两篇个人觉得讲得很好的回答。
我们用Haar小波做例子。
首先,介绍一个Haar尺度函数(又称为父小波),记为 ,
,如下图。
通过Haar尺度函数 ,可以得到Haar母小波
,
,如下图。
现在,对于一个 N 点的原始采样信号,如果我们可以用 N 个做了时域平移的Haar尺度函数和 N 个做了时域平移的Haar母小波,来逼近原信号,就可以得到用 N 个Haar尺度函数的系数和 N 个Haar母小波的系数。
从直观上看,Haar尺度函数只是一条线,而Haar母小波则是一个波。所以,Haar母小波所能表示出来的信息应该更加细致。因此,N 个Haar母小波组合起来,应该代表的是原始信号的细节部分,也就是高频部分;N 个Haar尺度函数组合起来,代表的是原始信号的粗略部分,也就是低频部分。
我们将N 个Haar母小波的系数称为高频系数,将N 个Haar尺度函数的系数称为低频系数。
所以,DWT的滤波功能,是通过利用尺度函数和母小波重构信号,获取重构系数来获得的,这已经定性地解决了本部分提出的问题。
关于DWT背后的数学原理,推荐两篇回答:
https://zhuanlan.zhihu.com/p/28575472
https://zhuanlan.zhihu.com/p/44217268
最后,由于DWT分解得到的是高频系数和低频系数,也就是用尺度函数以及母小波表示原信号的时候的一些重构系数,所以通过重构系数可以重构该信号,这被称为**小波分解的重构。**这也说明了小波分解是可逆的。
小波变换
小波变换的主旨:傅里叶变换将信号分解成为正弦波的叠加,傅里叶变换将信号分解成为正弦波的叠加。因此,如果要准确分析带突变的信号或图像,必须采用在时域和频域都含有定位信息的新方法
小波是一种快速衰减的、零均值的波形震荡,不像永远震荡的正弦波,小波持续的时间是有限的
中心频率: 尺度系数和频率之间是常系数倒数关系
- 较大的尺度系数会拉伸小波,对应的可表示低频
- 较小的尺度系数会压缩小波,对应的可表示高频
拉伸的小波可以捕捉信号中慢变的成分
而压缩的小波可以有效捕捉突变
连续小波、离散小波
他们的区别就是尺度缩放或者位移的方式不同
Author: Mrli
Link: https://nymrli.top/2019/07/29/傅里叶变换-小波变化/
Copyright: All articles in this blog are licensed under CC BY-NC-SA 3.0 unless stating additionally.