ACM-博弈论

ACM-博弈论（gambling）

博弈论：是二人或多人在平等的对局中各自利用对方的策略变换自己的对抗策略，达到取胜目标的理论。假设，双方每步都是最优决策

博弈论是研究互动决策的理论。博弈可以分析自己与对手的利弊关系，从而确立自己在博弈中的优势，因此有不少博弈理论，可以帮助对弈者分析局势，从而采取相应策略，最终达到取胜的目的。

巴什博弈

只有一堆n个物品，两个人轮流从这堆物品中取物，规定每次至少取一个，最多取m个。最后取光者得胜。

显然，如果n=m+1，1那么由于一次最多只能取m个，所以，无论先取者拿走多少个，后取者都能够一次拿走剩余的物品，后者取胜。因此我们发现了先手如何取胜的法则：除了先手取以外，之后每个双方回合时保证取走m+1个物品则能保证先手胜。

▲即如果n=(m+1)*r+s，（r为任意自然数，0<s<=m），那么先取者要拿走s个物品，如果后取者拿走k（<=m）个，那么先取者再拿走m+1-k个，结果剩下（m+1）（r-1）个，以后保持这样的取法，那么先取者肯定获胜。总之，要保持给对手留下（m+1）的倍数，就能最后获胜。

结论

• 编程解题的方法就是判断n是否能表示为(m+1)*r+s，找到这个m，和存在r，s
• s不为0，所以当n=(m+1)*r时，后手必胜

这个游戏还可以有一种变相的玩法：两个人轮流报数，每次至少报一个，最多报十个，谁能报到100者胜。

例题HDU1846——Brave Game，裸题

n为总价、总和，m为每次能取的大小

#include <bits/stdc++.h>
using namespace std;

int main(){
    int n, m;
    int t;
    cin >> t;
    while(t--){
        cin>>n >>m;
        int mod = n%(m+1);
        if (mod != 0) cout << "first" <<endl;
        else cout << "second" << endl;
    }
    return 0;
}

Public Sale

区别在于还存在n<m的情况，由于题目要求每次加价的幅度要在1～N之间，当价格大于或等于田地的成本价 M 时，主办方就把这块田地卖给这次叫价的人。，所以此时，第一次出价n+1~m都可以直接将物品买下，需要单独考虑

#include <bits/stdc++.h>
using namespace std;

int main(){
    int n, m;
    while (cin >> n>>m){
        if (n<m) {
            for(int i=n+1;i<=m;i++) 
                cout << i << " ";
            cout << endl;
        }else{
            int mod = n%(m+1);
            if (mod == 0) cout << "none"<<endl; //s=0，后手必胜
            else cout << mod << endl;   //存在s，即先手的Lele能买到
        }
    }
    return 0;
}

斐波那契博弈

有一堆个数为n的石子，游戏双方轮流取石子，满足：
1）先手不能在第一次把所有的石子取完；
2）之后每次可以取的石子数介于1到对手刚取的石子数的2倍之间（包含1和对手刚取的石子数的2倍）。

▲ 游戏规则动态化

这个游戏叫做Fibonacci Nim，肯定和Fibonacci数列：f[n]：1，2，3，5，8，13，21，34，55，89…有密切的关系。如果试验一番之后，可以猜测：先手胜当且仅当n不是Fibonacci数。换句话说，必败态构成Fibonacci数列。
就像“Wythof博弈”需要“Beatty定理”来帮忙一样，这里需要借助**“Zeckendof定理”（齐肯多夫定理）**：任何正整数可以表示为若干个不连续的Fibonacci数之和。定理的证明可以在这里看到，不过我觉得更重要的是自己动手分解一下。
e.g.比如，我们要分解83，注意到83被夹在55和89之间，于是把83可以写成83=55+28；然后再想办法分解28，28被夹在21和34之间，于是28=21+7；依此类推7=5+2，故；

如果n=83，我们看看这个分解有什么指导意义：假如先手取2颗，那么后手无法取5颗或更多，而5是一个Fibonacci数，如果猜测正确的话，（面临这5颗的先手实际上是整个游戏的后手）归纳得如果需要取走斐波那契数n，那么后手必胜，即那么一定是游戏的先手（此时为取5个的后手）取走这5颗石子中的最后一颗，而这个我们可以通过第二类归纳法来绕过，同样的道理，接下去先手取走接下来的后21颗中的最后一颗，再取走后55颗中的最后一颗，那么先手赢。需要注意到的是分解后不连续的若干个数单个的两倍都小于分解的最大数，即2n<m

▲如果n是斐波那契数，后手一定赢，如果不是，先手一定赢（先手胜当且仅当n不是斐波那契数列）。因为如果n是斐波那契数，那么先手取走数之后剩下的一定不是斐波那契数，后手必胜

例题hdoj 2516

#include <bits/stdc++.h>
using namespace std;

int arr[50];
// feibo
int main(){
    int n;
    arr[0] = 2,arr[1] = 3;
    for(int i=2;i<=50;i++) arr[i]=arr[i-1]+arr[i-2];
    
    while (cin >> n && n){
        int flag = 1;
        for(int i=0;i<=50;i++){
            if (arr[i]==n) flag=0,cout<<"Second win"<<endl;
            if (arr[i]>n) break;
        }
        if (flag) cout << "First win" <<endl;
    }
    return 0;
}

总结：

不需要深究博弈论数学原理，只需要知道结论，就可以写出代码。如，

巴什博弈：判断mod=n%(m+1)的结果s

斐波那契博弈：判断n是否为斐波那契数

威佐夫博弈

有两维各若干个物品(ak, bk)，两个人轮流从某一堆或同时从两堆中取同样多的物品，规定每次至少取一个，多者不限，最后取光者得胜。

这种情况下是颇为复杂的。我们用（ak，bk）（ak<=bk，k=0，1，2，.……n）表示两堆物品的数量并称其为局势，如果甲面对（0，0），那么甲已经输了，这种局势我们称为奇异局势。前几个奇异局势是：（0，0）、（1，2）、（3，5）、（4，7）、（6，10）、（8，13）、（9，15）、（11，18）、（12，20）。
可以看出，a0=b0=0，ak是未在前面出现过的最小自然数，而bk=ak+k，奇异局势有如下三条性质：

• 1.任何自然数都包含在一个且仅有一个奇异局势中。

  由于ak是未在前面出现过的最小自然数，所以有ak>ak-1，而bk=ak+k>ak-1+k-1=bk-1>ak-1。所以性质1。成立。

• 2.任意操作都可将奇异局势变为非奇异局势。
  事实上，若只改变奇异局势（ak，bk）的某一个分量，那么另一个分量不可能在其他奇异局势中，所以必然是非奇异局势。如果使（ak，bk）的两个分量同时减少，则由于其差不变，且不可能是其他奇异局势的差，因此也是非奇异局势。

• 3.采用适当的方法，可以将非奇异局势变为奇异局势。

从如上性质可知，两个人如果都采用正确操作，那么面对非奇异局势，先拿者必胜；反之，面对奇异局势，则后拿者取胜。

Betty定理:…

▲那么任给一个局势（a，b），怎样判断它是不是奇异局势呢？我们有如下公式：

ak =[k（1+V5）/2]，bk=ak+k（k=0，1，2，.……n方括号表示取整函数）奇妙的是其中出现了黄金分割数（1+V5）/2=1.618…，因此，由ak，bk组成的矩形近似为黄金矩形，由于2/（1+V5）=（V5-1）/2，可以先求出j=[a（V5-1）/2]，若a=[（1+V5）/2]，那么a=aj，bj=aj+j，若不等于，那么a=aj+1，bj+1=aj+1+j+1，若都不是，那么就不是奇异局势。然后再按照上述法则进行，一定会遇到奇异局势。===> 如果(b-a)*(sqrt(5.0)+1)/2 == a的话就是奇异局势

例题poj 1067，裸题

#include <bits/stdc++.h>
using namespace std;

int main(){
    int a, b, c;
    while(cin >> a >> b){
        if (a>b) swap(a,b);
        int c = floor((b-a)*(sqrt(5.0)+1)/2);
        if (a==c) cout << 0 << endl;
        else    cout << 1 << endl;
    }
    return 0;

}

尼姆博弈（Nim）

有n堆各若干个物品，两个人轮流从某一堆取任意多的物品，规定每次至少取一个，多者不限，最后取光者得胜。

以n=3为例子，这种情况最有意思，它与二进制有密切关系，我们用（a，b，c）表示某种局势，首先（0，0，0）显然是奇异局势，无论谁面对奇异局势，都必然失败。第二种奇异局势是（0，n，n），只要与对手拿走一样多的物品，最后都将导致（0，0，0）。仔细分析一下，（1，2，3）也是奇异局势，无论对手如何拿，接下来都可以变为（0，n，n）的情形。

然而这并不是博弈的重点，博弈之王道乃是SG值，当sg值为0的时候，就是输，不为0就是赢；

SG值：一个点的SG值就是一个不等于它的后继点SG值的且大于等于零的最小整数。

• 不属于它后继点SG值集的值

大概的意思就是：在步骤允许的情况下，与前面一个必败点的差（也就是说这个差是规定的、能走的、其中一个步数）！
后继点：也就是按照题目要求的走法（比如取石子可以取的数量，方法）能够走一步达到的那个点。（sg值的理解很抽象。需要多画画）

举个栗子：比如一堆石子，我们可以取任意个，那么x个石子的石子的sg值是多少呢？可以知道，0个石子sg为0，1的时候我们可以取一个，剩下0，0的sg是0(SG(0)=0)，那么mex(0)就是1，所以1的sg为1(SG(1)=1)。即SG(1) = mex{SG(0)}=mex{0}=1

例题hdoj 1847

#include <bits/stdc++.h>
using namespace std;

int arr[15],sg[1005];
int mex(int x){
    if(sg[x] != -1) return sg[x];
    // 记忆化搜索,如果存在直接返回
    bool vis[1005];
    for(int i=0; i<1005;i++) vis[i] = false;
    for (int i =0;i<=10;i++) {
        int temp = x - arr[i];
        if (temp<0) break;
        // SG值为非负整数
        sg[temp] = mex(temp);
        // 需要递归调用，分治求出小的部分的结果
        vis[sg[temp]] = true;
    }
    for (int i =0;;i++)
        if(!vis[i]) {
            // 找到最小的数，mex{0,1,2}=3，mex{1,2,3}=0，mex{0,1,3}=2；
            sg[x]=i;
            break;
        }
    return sg[x];
}


int main(){
    int n;
    arr[0] = 1;
    for (int i = 1; i<=10; i++)
        arr[i] = arr[i-1]*2;
    while(cin >> n){
        memset(sg,-1,sizeof(sg));
        if (mex(n)) cout << "Kiki" <<endl;
        else cout << "Cici" << endl;
    }
    return 0;
}

组合博弈：（博弈的精华）

组合博弈无疑是对sg值的熟练操作例如：有n堆石子，每次可以从第1堆石子里取1颗、2颗或3颗，可以从第2堆石子里取奇数颗，可以从第3堆及以后石子里取任意颗.……我们可以把它看作3个子游戏，第1个子游戏只有一堆石子，每次可以取1、2、3颗，很容易看出x颗石子的局面的SG值是×%4。第2个子游戏也是只有一堆石子，每次可以取奇数颗，经过简单的画图可以知道这个游戏有x颗石子时的SG值是×%2。第3个游戏有n-2堆石子，就是一个Nim游戏。对于原游戏的每个局面，把三个子游戏的SG值异或一下就得到了整个游戏的SG值，然后就可以根据这个SG值判断是否有必胜策略以及做出决策了。其实看作3个子游戏还是保守了些，干脆看作n个子游戏，其中第1、2个子游戏如上所述，第3个及以后的子游戏都是“1堆石子，每次取几颗都可以”，称为“任取石子游戏”，这个超简单的游戏有x颗石子的SG值显然就是x。

SWPU-ACM每周算法讲堂-博弈论入门

计算机博弈大赛

蒙特卡洛方法

由冯·诺依曼、乌拉姆等人发明，因蒙特卡洛赌场而闻名，一种基于概率的方法的统称。

一种让人感觉“我去，这也行”的方法——根据大概率逼近真实结果的方法

拉斯维加斯（Las Vegas）方法——找老婆（必须要精确找到那一个答案，其他都不行。采样越多，越有机会找到最优解）

• 找1W人才能准确确定

蒙特卡罗（Monte Carlo）方法——民意调查（一直在找，找的是逐渐贴近于最优解的结果。当样越多，越近似最优解）

• 找了2K人大致能确定了

相关方法：

• 蒙特卡罗算法、蒙特卡罗模拟、蒙特卡罗过程
• 蒙特卡罗搜索树一—AlphaGo

工作原理：

• 不断抽样（中心极限定理，n->∞）
• 逐渐逼近（依概率逼近）

蒙特卡洛树搜索 （MCTS，Monte Carlo tree search）

一种用于某些决策过程的启发式搜索算法，最引人注目的是在游戏中的使用

双人有限零和顺序游戏

MCTS运行所在的框架/环境是一个游戏，它本身是一个非常抽象和宽泛的概念，因此这里我们只关注一种游戏类型：双人有限零和顺序游戏。这个名词一开始听起来会有些复杂，但是实际上非常简单，现在来让我们将它分解一下：

• 游戏：意味着我们在一种需要交互的情境中，交互通常会涉及一个或多个角色
• 有限：表明在任意时间点，角色之间存在的交互方式都是有限的
• 双人：游戏中只有两个角色
• 顺序：玩家依次交替进行他们的动作
• 零和：参与游戏的两方有完全相反的目标，换句话说就是，游戏的任意结束状态双方的收益之和等于零

我们可以很轻松的验证，围棋、国际象棋和井字棋都是双人有限零和顺序游戏：有两位玩家参与，玩家能进行的动作总是有限的，双方的游戏目标是完全相反的（所有游戏的结果之和等于0）。

如何表示一个游戏

从程序员的角度来看，可以用一种常见的数据结构以来表示游戏——游戏树。

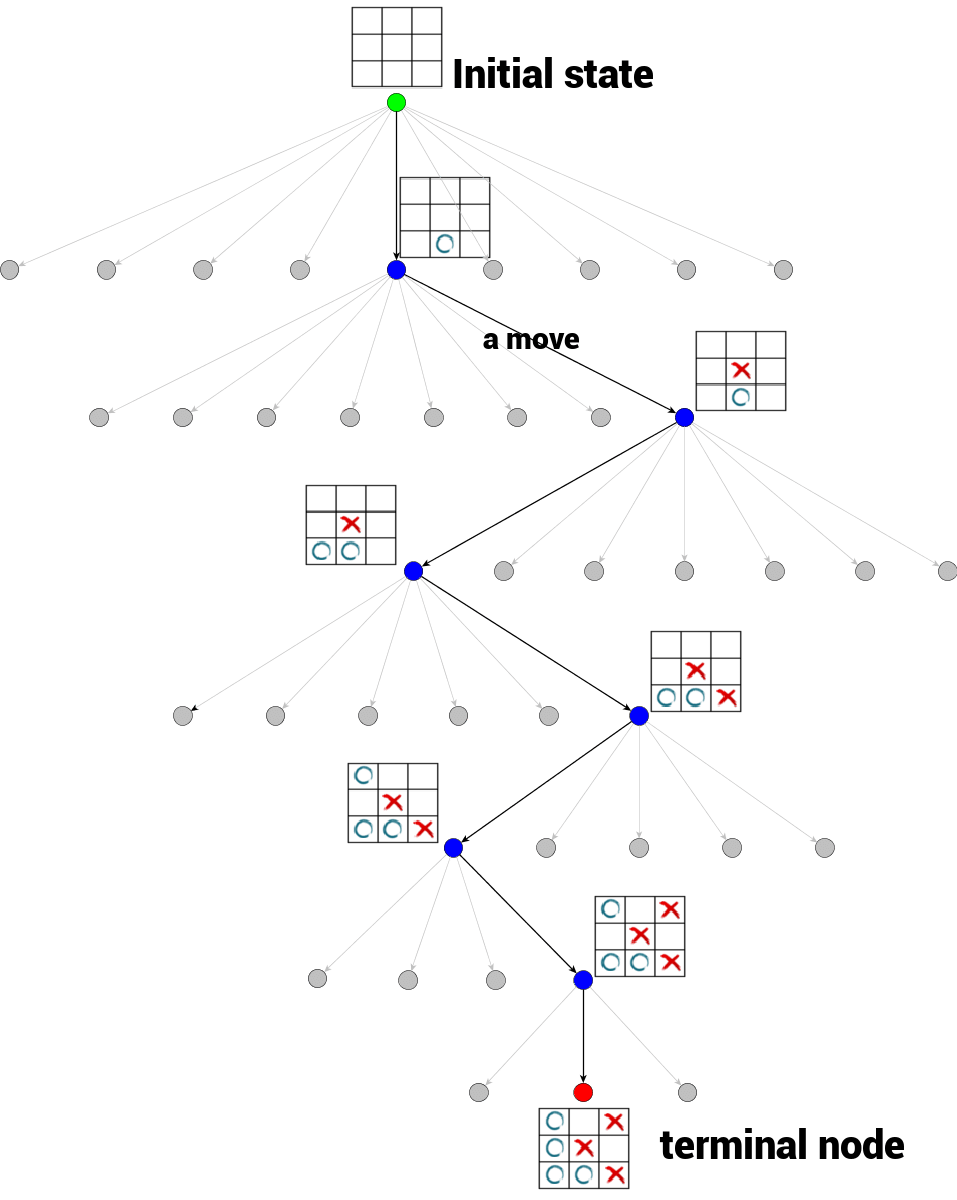
游戏树是一个数，其中每一个节点代表游戏的一个确定状态。从一个节点到该节点的一个子节点（如果存在）是一个移动。节点的子节点数目称为分支因子。游戏树的根节点代表游戏的初始状态。游戏树的终端节点是没有子节点的节点，至此游戏结束，无法再进行移动。终端节点的状态也就是游戏的结果（输/赢/平局）。

游戏树是一种递归的数据结构，每次选择完最佳的下一步时，会移动到下一个子节点，而这个子节点又是它子树的根节点。因此我们可以把一局游戏视为“最佳下一步”的一个问题序列，每一次都可以由一个不同根节点的游戏树表示。通常在实际应用中，我们不需要记住到当前状态的路径，因为这不是当前游戏状态的关注点。