蒙特卡洛树搜索MCTS

跟围棋的关联

AlphaGo Zero

蒙特卡洛树搜索——内含用于树遍历的 PUCT 函数的某些变体
残差卷积神经网络——其中的策略和价值网络被用于评估棋局，以进行下一步落子位置的先验概率估算。
强化学习——通过自我对弈进行神经网络训练

AlphaGo Zero跟AlphaGo的最大区别是抛弃人类棋谱的，完全通过自我对弈来学会下棋的，并且仅用40小时就到达了AlphaGo的棋力。

过程是这样，首先生成棋谱，然后将棋谱作为输入训练神经网络，训练好的神经网络用来预测落子和胜率。如下图：

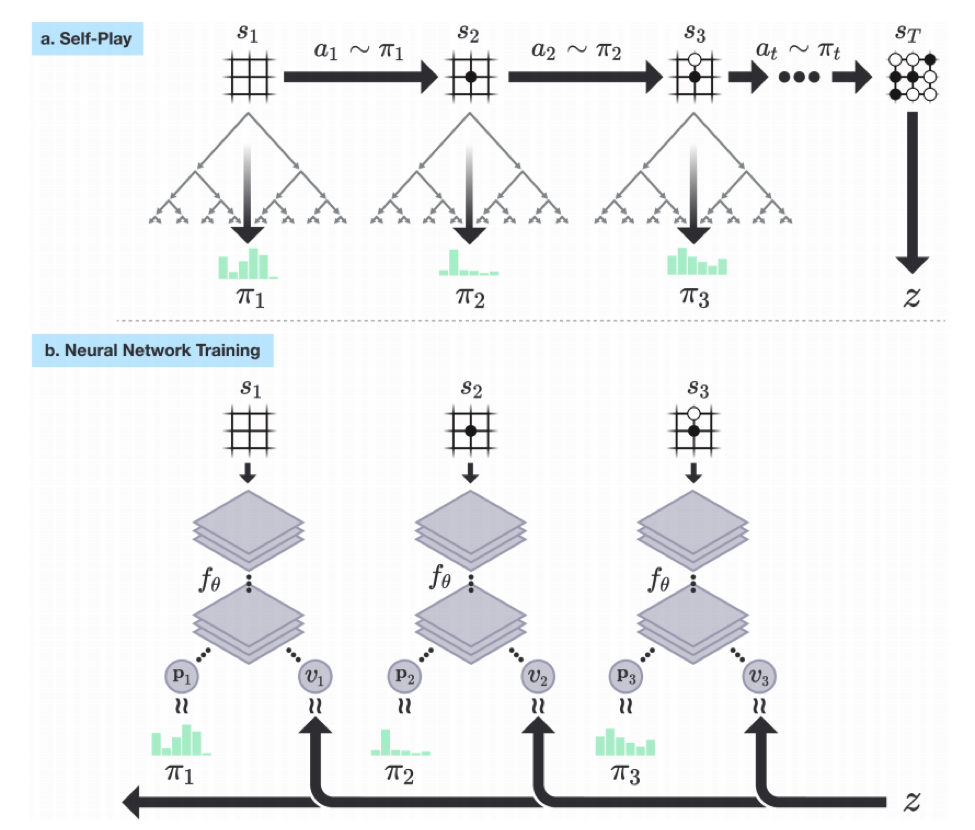
2018031214442364

在AlphaGo Zero中蒙特卡洛树搜索主要是用来生成棋谱的

蒙特卡洛树搜索

Q:MCTS干了什么?

A:给出一个「游戏状态」并选择「胜率最高的下一步」

适用于有限两人零和回合制游戏

MCTS算法是一种决策算法，每次模拟（simulation）分为4步：

Tree traversal(树的遍历):
$UCB1(S_{i})=\overline{V_{i}}+c \sqrt{\frac{\log N}{n_{i}}}, c=2$
其中，表 $\overline{V_{i}}$ 示 $S_i$ 状态的平均value(下面会进一步解释）
Node expansion(拓展节点)
Rollout (random simulation)(模拟)
Backpropagation(反向传播)

蒙特卡洛计算过程

UCB(Upper Confidence Bounds置信上限)其实就是UCT(UCB for Tree)中需要计算的值，而UCT是根据UCB值来迭代的算法

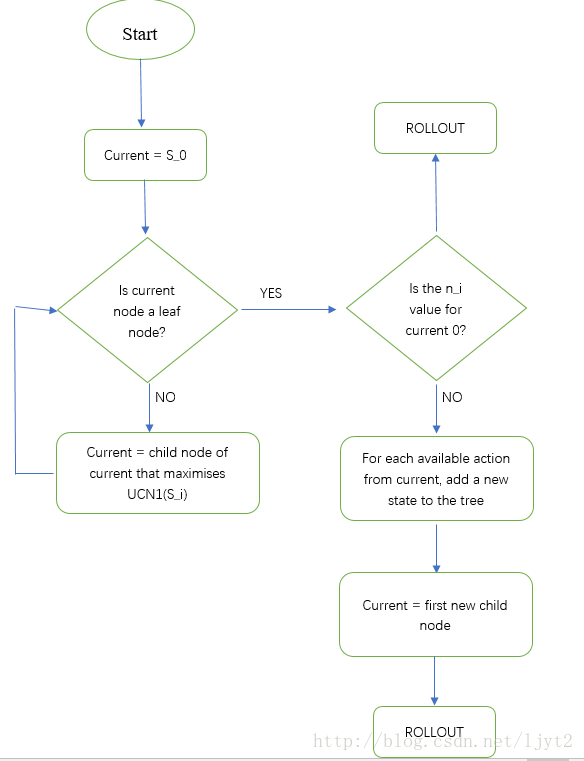
第一、二步的流程（遍历、拓展节点）：

1.从状态S0开始，要在下面两个动作中进行选择（假设只有两个动作可选），选择的标准就是 $UCB1(S_{i})$ 值，选择最大化 UCT 的节点作为下一个节点。初始情况两个 $UCB1(S_{1})=UCB1(S_{2})=\infty$ ,按顺序选择S1
2.判断目前的结点S1(current node)是不是叶节点，这里叶节点是指其没有被展开（expansion）过。
3.接下来，按照流程图，需要判断结点S1被访问的系数是否为0。是0，则要进行Rollout。(Rollout其实就是在接下来的步骤中每一步都随机采取动作，直到停止点（围棋中的对局结束），得到一个最终的value。)==>假设Rollout最终值为20.
4.Backpropagation，即利用Rollout最终得到的value来更新路径上每个结点的T,N值。(之后把Rollout的结果删除：MCTS的想法就是要从出S0发不断的进行迭代，不断更新结点值，直到达到一定的迭代次数或者时间。)
5.如果没有达到一定的迭代次数或者时间，继续从根节点进行1-4

20171024211039397

第三步rollout模拟:

/*这个函数接受一个表示博弈状态的参数，然后返回下一步行动。实际上，它被设计得非常快，从而可以让很多模拟快速进行——默认的 rollout policy 函数是一个均衡分布的随机数生成函数。*/
Rollout(S_i):
    loop forever:
     /* 如果当前状态结点是个终止结点 */
     if S_i is a terminal state:
         /* 那么直接返回它的value值*/
         return value(S_i)
     /* 找到下一个动作 */
     A_i = random(available-actions(S_i))
     /* 选择下一个状态进行拓展 */
     S_i = simulate(A_i,S_i)

4.反向传播：从子节点的结果传到根节点

例子说明见:蒙特卡洛树搜索（MCTS）算法-计算过程，视频讲解见B站:【MCTS】Youtube上迄今为止最好的蒙特卡罗树搜索讲解

还有个搜索算法：极大极小法（minimax）。这个策略假定你的对手发挥了最好的博弈水平，然后以此调整策略来最大化你的收益。简单地说，给定状态，你想要找到一个能产生最大收益的 move ，假定你的对手想要最小化你的收益（最大化他自己的收益）。因此，名字叫作极小化极大。

极小化极大算法的最大劣势是，需要扩展整个博弈树。对于分支因子较高的博弈（例如围棋或者国际象棋），这会导致庞大的博弈树从而失败，所以一般MinMax算法外还要加上alpha-beta剪枝。

UCT算法——树的置信上限(UCB for Trees)

Upper Confidence Bounds(置信上限)

UCB1是一个让我们从已访问的节点中选择下一个节点来进行遍历的函数，也是MCTS的核心函数。

UCB1(v_{i}, v)=\frac{Q(v_{i})}{N(v_{i})}+c \sqrt{\frac{\log (N(v))}{N(v_{i})}}

其中v为当前节点，Vi为其子节点。

exploitation component(利用)

第一部分是，也称作exploitation component。 Q(Vi)为子节点获胜次数，N(Vi)为子节点参与模拟的次数

可以看做是子节点Vi的胜率估计（总收益/总次数=平均每次的收益）。但是不能只选择胜率高的下一步，因为这种贪婪方式的搜索会很快导致游戏结束，这往往会导致搜索不充分，错过最优解。

举个简单的例子。现在假设MCTS的UCT函数只用了探索成分，从根节点开始，我们对所有子节点进行了一次模拟，然后在下一步中只访问至少赢了一次的子节点。那么在第一次模拟中那些不幸未被选中的节点（实际中rollout策略函数通常是随机的）将会被立刻抛弃

exploration component(探索)

c \sqrt{\frac{\log(N(v))}{N(v_{i})}}$$，这个成分更倾向于那些想对较少被探索的节点N(Vi)小。 参数c是exploitation和exploration之间的折中系数。 ### MCTS的终止 终止条件(or)： - 达到一定的迭代次数 - 达到规定的搜索时间 当MSCT程序结束时，最佳的移动通常是访问次数最多的那个节点，也是UCT最大的点。 ## 参考: [深度学习入门：AlphaGo Zero蒙特卡洛树搜索](https://blog.csdn.net/mergerly/article/details/83788862) [蒙特卡洛树搜索（MCTS）算法-计算过程](https://blog.csdn.net/ljyt2/article/details/78332802) [【MCTS】Youtube上迄今为止最好的蒙特卡罗树搜索讲解](https://www.bilibili.com/video/av67847675?from=search&seid=7487786042631726209) [AI如何下棋？直观了解蒙特卡洛树搜索MCTS！！！](https://www.bilibili.com/video/BV1JD4y1Q7mV?from=search&seid=6045698802301050730)——整体讲的很好，汇总了百度能搜到的大部分知识点 ## 代码实现文档: [python实现的基于蒙特卡洛树搜索(MCTS)与UCB的五子棋游戏](https://blog.csdn.net/white_gl/article/details/56521880) [mctspy：井字棋-蒙特卡洛树搜索算法的python实现](https://github.com/int8/monte-carlo-tree-search) --- 蒙特卡洛树搜索（MCTS）仅展开根据 UCB 公式所计算过的节点，并且会采用一种自动的方式对性能指标好的节点进行更多的搜索。具体步骤概括如下： 1.由当前局面建立根节点，生成根节点的全部子节点，分别进行模拟对局； 2.从根节点开始，进行最佳优先搜索； 3.利用 UCB 公式计算每个子节点的 UCB 值，选择最大值的子节点； 4.若此节点不是叶节点，则以此节点作为根节点，重复 2； 5.直到遇到叶节点，如果叶节点未曾经被模拟对局过，对这个叶节点模拟对局；否则为这个叶节点随机生成子节点，并进行模拟对局； 6.将模拟对局的收益（一般胜为 1 负为 0）按对应颜色更新该节点及各级祖先节点，同时增加该节点以上所有节点的访问次数； 7.回到 2，除非此轮搜索时间结束或者达到预设循环次数； 8.从当前局面的子节点中挑选平均收益最高的给出最佳着法。 由此可见 UCT 算法就是在设定的时间内不断完成从根节点按照 UCB 的指引最终走到某一个叶节点的过程。而算法的基本流程包括了选择好的分支（Selection）、在叶子节点上扩展一层（Expansion）、模拟对局（Simulation）和结果回馈（Backpropagation）这样四个部分。 UCT 树搜索还有一个显著优点就是可以**随时**结束搜索并返回结果，在<u>每一时刻，对 UCT 树来说都有一个相对最优的结果</u>。 https://blog.csdn.net/white_gl/article/details/56521880