高性能问题: 你需要在一秒内完成全部的命令 ,然后将查询结果按顺序得出后传回,命令如下:
Add i j,i和j为正整数,表示第i个仓库增加j个库存(j不超过220)Sub i j,i和j为正整数,表示第i个仓库减少个库存(j不超过220)Query i j,i和j为正整数,i<=j,表示询问第i到第个仓库的总库存;End 表示结束,这条命令在每组数据最后出现;
思路一:用array去存储每个仓库的容量,在查询时用循环取出(L,R)的总容量。此时Update为O(1),Query为O(N)
思路二:前缀数组和 :在array1储存每个仓库容量的同时维护array2来记录前n个仓库的总容量,当计算某个区间的容量(L,R)可以通过s[R]-s[L-1]求出。此时Query为O(1),但Update为O(N)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 #include <bits/stdc++.h> using namespace std ;const int maxn = 1e3 ;int arr[maxn];int main () int n; cin >> n; int tmp; cin >> tmp; arr[1 ] = tmp; for (int i = 2 ; i <= n; i++) { cin >> tmp; arr[i] = tmp + arr[i-1 ]; } for (int i = 1 ; i <= n; i++) { cout << arr[i] <<endl ; } cout << arr[4 ] - arr[2 -1 ] << endl ; return 0 ; }
思路三:树状数组:Update和Query的时间复杂度进行折中后都为O(logN)
又叫二叉索引树,最早是为了解决数据压缩里的累积频率问题,现多用来解决数组区间查询问题的数据结构,即高效解决数列的前缀和 、区间和 问题。
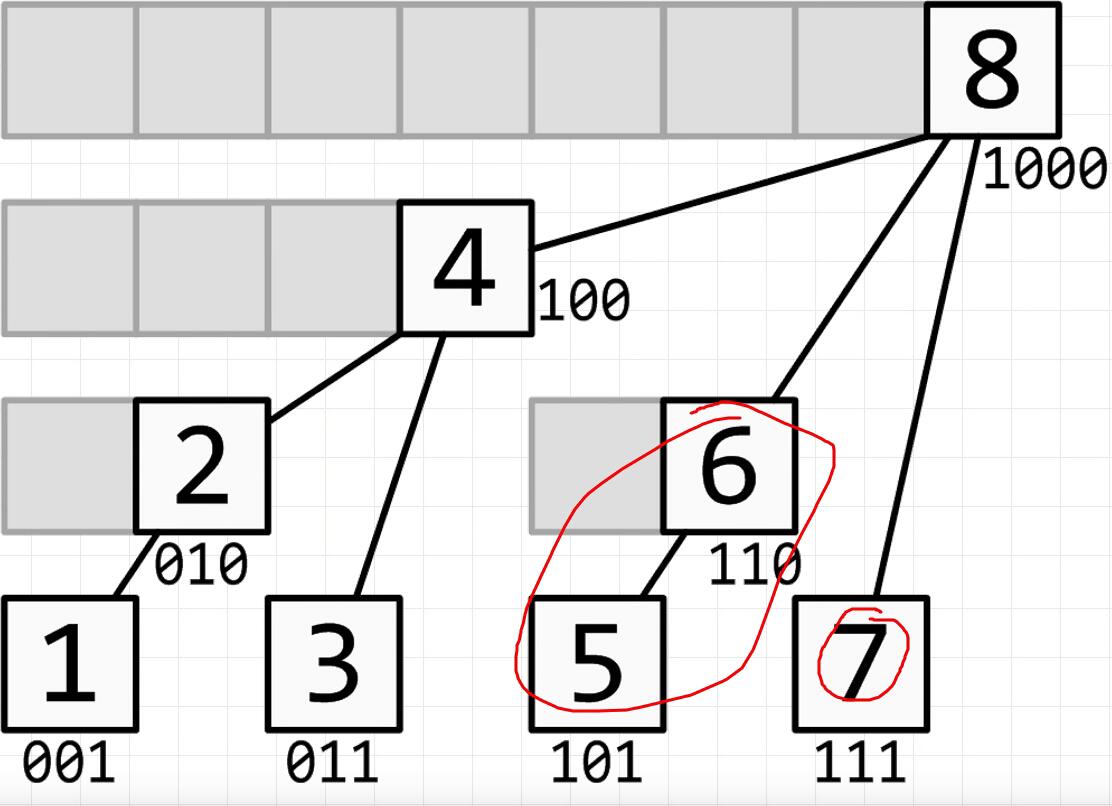
核心:将一个数拆分成若干个二进制数相加,原理:每一个数都有二进制表示,即所有数都可以表示成x个不同的2的幂之和。
做法:找到二进制最后低一位1表示的数。n&-n找到n最右边的1。
举个栗子:
因此树状数组的维护更新过程如下:已知i=6i 最右边的1,即得到l o w b i t = ( 10 ) 2 = ( 2 ) 10 lowbit=(10)_{2}=(2)_{10} l o w b i t = ( 1 0 ) 2 = ( 2 ) 1 0 i ′ = i − l o w b i t = ( 0110 ) 2 − ( 0010 ) 2 = ( 0100 ) 2 i'= i - lowbit = (0110)_{2}-(0010)_{2}=(0100)_{2} i ′ = i − l o w b i t = ( 0 1 1 0 ) 2 − ( 0 0 1 0 ) 2 = ( 0 1 0 0 ) 2 i ′ = 6 − 2 = ( 4 ) 10 i'=6-2=(4)_{10} i ′ = 6 − 2 = ( 4 ) 1 0 i 最右边的1,即得到了l o w b i t = ( 100 ) 2 = ( 4 ) 10 lowbit=(100)_{2}=(4)_{10} l o w b i t = ( 1 0 0 ) 2 = ( 4 ) 1 0 i ′ = i − l o w b i t = ( 0100 ) 2 − ( 0100 ) 2 = ( 0000 ) 2 i'= i - lowbit =(0100)_{2}-(0100)_{2}=(0000)_{2} i ′ = i − l o w b i t = ( 0 1 0 0 ) 2 − ( 0 1 0 0 ) 2 = ( 0 0 0 0 ) 2
找到( n ) 2 (n)_2 ( n ) 2 ( n 1 ) 2 (n1)_2 ( n 1 ) 2
更新n ′ = ( n ) 2 − ( n 1 ) 2 n'=(n)_2 - (n1)_2 n ′ = ( n ) 2 − ( n 1 ) 2
如果( n ′ ) 2 (n')_2 ( n ′ ) 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 N = 1e6 + 5 arr = [0 ] * N def add (i, j) : ''' 修改第i仓库Ci。但注意执行某个仓库的update操作,后面所有仓库都得更新 ''' while i <= N: arr[i] += j i += i&-i def sub (i, j) : add(i, -j) def sum (i) : ''' 通过Ci求出1-i仓库的总库存 S[6] = C[6] + C[4], 推导如下: 如果i=6,那么 ans += c[6] , i <- i-2 = 6-2 = 4, ans += c[4] , i <- i-4 = 4-4 = 0 ∴ans = c[6] + c[4] = A[6]+A[5]+A[4]+A[3]+A[2]+A[1] ''' ans = 0 while i > 0 : ans += arr[i] i -= i&(-i) return ans def query(i, j); ''' 查询某个区间的总库存,sum(i, j) = S(R) - S(L-1) ''' return sum(j) - sum(i-1 )
符号说明:
Ai:第i个仓库的库存数
Ci:所构建的数的第i个节点的值,C[i] = A[i-lowbit(i)+1] + …+A[i]
Si:第1个仓库到第i个仓库库存数之和
Ans(i,j):显然就等于S R − S L − 1 S_{R}-S_{L-1} S R − S L − 1
一.从原数组A[],维护树状数组C[]
▲lowbit又叫子叶数,表示了有多少个A[]相加,C[i]表示从C[i] = A[i-lowbit(i)+1] + …+A[i] (<===>C[i] = A[i-2^x+1] + … + A[i]),
For Example: i=6
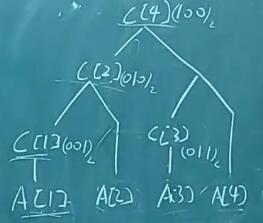
树状数组 ——黑板讲解,NICE
树状数组算法 ——初步了解,有些点讲的并不那么纤细
洛谷: P3374 【模板】树状数组 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 #include <bits/stdc++.h> #define N 500000 + 5 using namespace std ;int c[N];void add (int i, int k) int index = i; while (index<=N){ c[index] += k; index += index&(-index); } } int sum (int n) int index = n; int ans = 0 ; while (index){ ans += c[index]; index -= index&(-index); } return ans; } int query (int l, int r) return sum(r) - sum(l-1 ); } int main (int argc, char const *argv[]) ios::sync_with_stdio(false ); int n, m; cin >> n >> m; for (int i = 1 ; i <= n; ++i){ int val; cin >> val; add(i, val); } for (int i = 0 ; i < m; ++i){ int op; int x, k; cin >> op >> x >> k; if (op==1 ) add(x, k); else cout << query(x, k) << endl ; } return 0 ; }
在求解前缀和、区间和问题上,两者是没有差别的,并且树状数组的空间复杂度更低。但是线段树还有更多的功能,比如求取区间最大值。
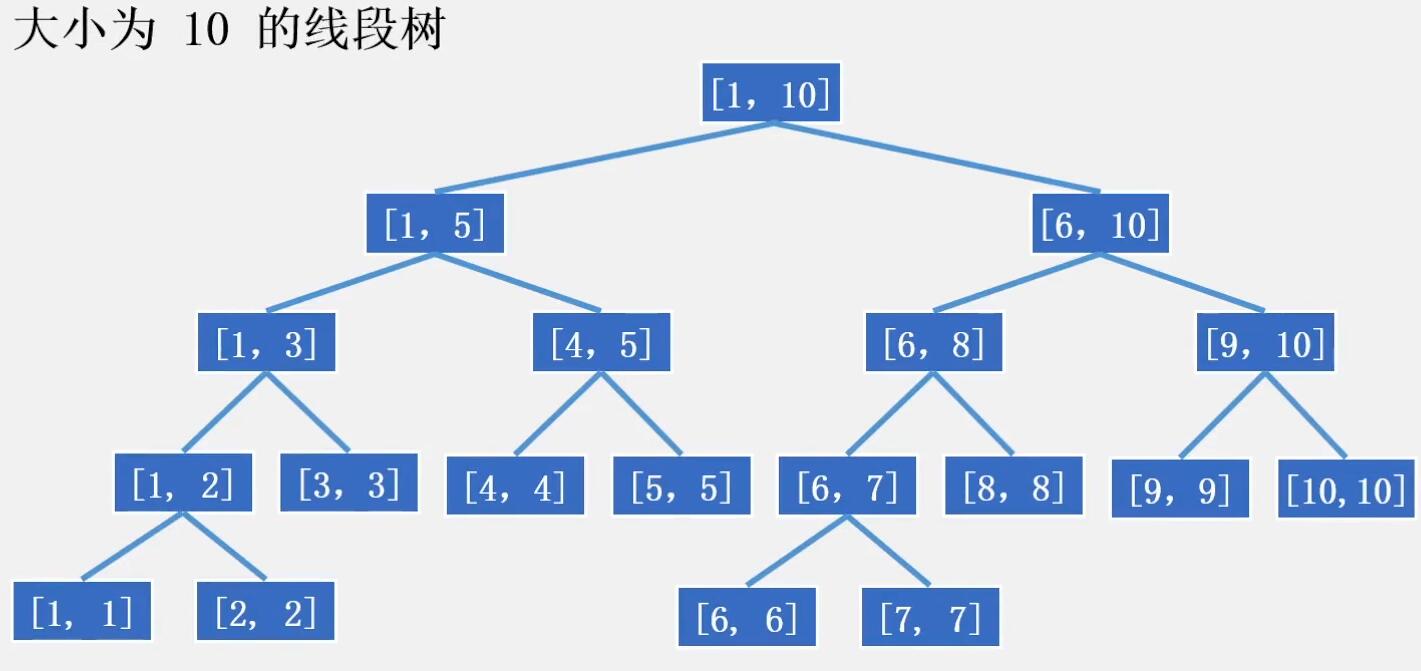
完满二叉树(Full Binary Tree)
每个节点维护一个闭区间1,r 的信息。
根节点表示[1,n]的信息。如果1=r那就是叶子结点.
如果1<r那就是内部节点,它有两个子节点[1,(1+r)/2],[(1+r)/2+1,r].
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 void update (int x) sum[x]= sum[x*2 ] + sum[x*2 +1 ]; } void build (int 1 ,int r,int x) if (l==r){ sum[x]=a[1 ]; return ; } int mid=(1 +r)>〉1 ; build(1 ,mid,x*2 ); build(mid+1 ,r,x*2 +1 ); update(x); } int query (int A,int B,int 1 ,int r,int x) if (A<=1 &&r<=B) return sum[x]; int mid=(1 +r)>>1 ,ans=0 ; if (A<=mid) ans+=query(A,B,1 ,mid,x*2 ); if (mid<B) ans+=query(A,B,mid+1 ,r,x*2 +1 ); return ans; } int change (int pos,int v,int 1 ,int r,int x) if ( l==r){ sum[x]=v; return ; } int mid=(1 +r)>>1 ; if (pos<=mid) change(pos,v,1 ,mid,x*2 ); else change(pos,v,mid+1 ,r,x*2 +1 ); update(x); }
节点数:假设线段树处理的数列长度为n,即根节点的区间为[1,n].那么结点数不超过2n个.因此线段树的空间复杂度是0(n)。是完满二叉树(Full Binary Tree),但一般申请4*n的空间大小
深度:可以看作满二叉树,深度不超过log2(n-1)+1
线段树能把区间上的任意一条长度为L的线段都分成不超过2*log(L)条线段。
注意:
由于链表表示的内存是不连续的,且申请指针比较费时间,所以采用数组矩阵的形式存储。
数组存储也有一点不好,因为线段树并不是真正的完全二叉树。
例题:
Q:对于第i个数,我们要统计前面有多少个数大于a[i]。
e.g.如果一个值为1,一个值为108,那么要开10 8大小
Solve: 10^9范围太大了,因此我们先要对n个数进行离散化 。离散化的过程,就是对n个数进行排序,最小的数赋值为1 ,第二小的赋值为2 ,以此类推,这样n个数的取值范围就在[1,n]中了。
e.g.上面的情况,将会把1–>1,10^8–>2,那么只要开长度为2的线段树就够了
1 2 3 4 5 6 7 8 9 10 int cnt=0 ;for (int i=1 ;i<=n;i ++) bin[++cnt]=a[i]; sort(bin+1 ,bin+n+1 ); cnt=unique(bin+1 ,bin+cnt+1 )-bin-1 ; for (inti=1 ;i<=n;i ++) a[i]=lower_bound(bin+1 ,bin+cnt+1 ,a[i])-bin;
参考:
高中信息学竞赛线段树与树状数组 ——万门教育
SWPU-ACM每周算法讲堂-线段树入门(一)