认真学次DP——动态规划

动态规划DP

一般算法面试题解决最优化问题，有两种解决途径：暴力枚举、或者DP，由于其灵活和高效，无数程序员为它着迷，大厂面试也是必考。

但是，动态规划形式上非常多变，本质上没有套路，问题不同，动态规划的迭代方程就不同。而有些问题，对于计算机科学家，都难以找到迭代方程。因此，对于平平常常的我们，刷算法题时想不出动态规划的解法，也大可不必气馁。

DP组成——三个条件

某个问题是否能应用动态规划，通常需要满足 3 个条件：

1. 具有最优子结构
2. 具有无后续性
3. 具有重复子问题

最优子结构性质：只需求得子问题的最优解后，原问题的最优解最能推导出来，这表明此问题具备最优子结构性质！

**后续状态无关性：**在具体的问题中就是，子数组的最大和，与后面的红块无关

**重复子问题：**使用暴力枚举会对很多子问题重复计算，也就是说这个问题具备重复子问题特性。而DP数组的存在可以很好的处理重复子问题计算。

DP组成——三个要素

• 最优子结构
• 边界
• 状态转移方程式

**最优子结构：**只需求得子问题的最优解后，原问题的最优解最能推导出来，这表明此问题具备最优子结构性质！

边界：确定起始和终止边界

**状态转移方程式：**在某个状态下找到下一步的最佳计算结果

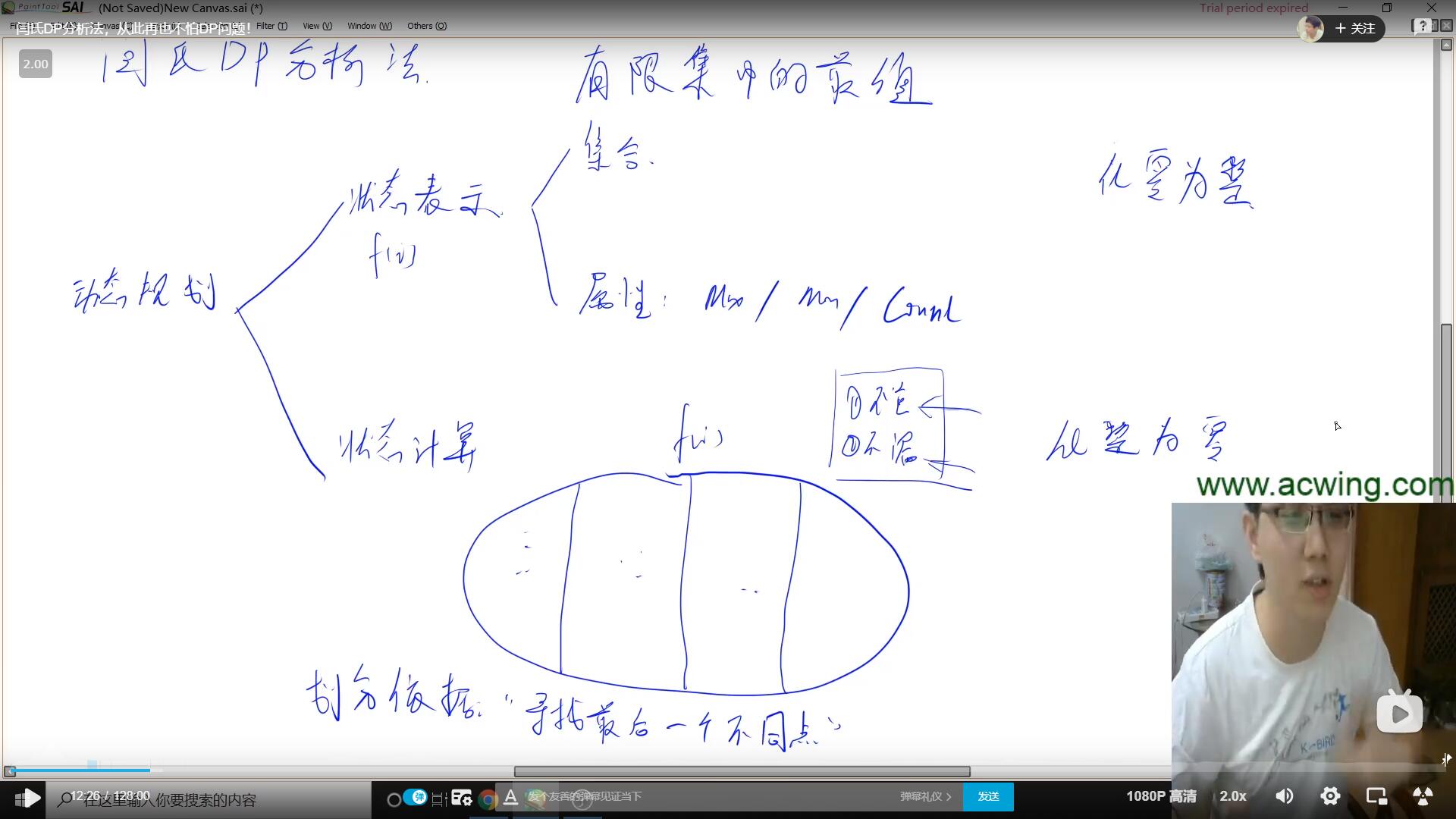
▲.其中最重要的就是找到确定 状态表示f(v) 和 状态转移计算。目的是：讲究在一个有限集合的中找一个最值

状态表示f(v)：——化零为整

• 集合
• 属性： 最大、最小、count数量

状态转移计算：——化整为零

划分依据：寻找最后一个不同点。 讲究不重复、不遗漏

问题剖析

最常见的来讲解DP算法的是背包问题， 在此我们列出多个比较经典的题目： 国王和金矿、最大子数组的和、背包问题

国王和金矿

最大子数组的和：

题解：https://leetcode-cn.com/problems/lian-xu-zi-shu-zu-de-zui-da-he-lcof/solution/mian-shi-ti-42-lian-xu-zi-shu-zu-de-zui-da-he-do-2/ ——为何在nums数组上直接做修改

class Solution {
    public int maxSubArray(int[] nums) {
        int sz = nums.length;
        if ( sz == 0 ) return 0;
        int maxSum = nums[0];
        for (int i = 1; i < sz; i++) {
            int pre = nums[i-1] > 0 ? nums[i-1] : 0;
            nums[i] = nums[i] + pre;
            if (maxSum < nums[i]) {
                maxSum = nums[i];
            }
        } 
        return maxSum;
    }
}

最长公共子序列问题

题目的要求是，从两个字符串中找到最长的公共子序列，出现先后顺序要求一致， 但是不要求连续。

所以下面解法定义的dp数组为，状态到text1的i字符、text2的j字符时最长的公共子序列的长度，如果当前的两个字符c1 == c2则需要在此基础上+1， 否则记为之前的两个的最大。

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int len1 = text1.length();
        int len2 = text2.length();
        int [][]dp = new int[len1+1][len2+1];
        for (int i = 0; i < len1; i++) {
            char c1 = text1.charAt(i);
            for (int j = 0; j < len2; j++) {
                char c2 = text2.charAt(j);
                if ( c1 == c2 ){
                    dp[i + 1][j + 1] = dp[i][j] + 1;
                }else{
                    dp[i + 1][j + 1] = Math.max(dp[i][j + 1], dp[i + 1][j]);
                }
            }
        }
        return dp[len1][len2];
    }
}

01背包问题

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e4;
/* 01背包问题 */
pair<int,int> wv[maxn];
int N; // 物品数量
int W; // 背包重量

int dp[maxn][maxn]; //2.多了个记忆数组(称为DP数组)

// 逆序推导
void solve(){
    ios::sync_with_stdio(false);
    cin >> N;
    for(int i=0 ; i <N ; i++) cin >> wv[i].first >> wv[i].second;
    cin >> W;
    for( int i= N-1 ; i >= 0 ; i--){		
        for( int j=0;j<= W ; j++){			
            if( j < wv[i].first ) dp[i][j] = dp[i+1][j];
            else
            	dp[i][j] = max( dp[i+1][j] , dp[i+1][j - wv[i].first] + wv[i].second);
        }
    }
    cout << dp[0][W] <<endl;
}


// 顺序推导
void solve(){
    ios::sync_with_stdio(false);
    cin >> N;
    for(int i=0 ; i <N ; i++) cin >> wv[i].first >> wv[i].second;
    cin >> W;

    for( int i= 0 ; i < N ; i++){			// i为遍历第i个物品
        for( int j=0;j<= W ; j++){			// j为背包可用重量
            if( j < wv[i].first ) dp[i+1][j] = dp[i][j];
            else
            dp[i+1][j] = max( dp[i][j] , dp[i][j - wv[i].first] + wv[i].second);
        // 推导式也变了,下一行的依据上一行写成dp[i+1][j] = ...
        }
    }
    cout << dp[N][W] <<endl;
    // 输出的结果变了
}

int main(){
    solve();
    return 0;
}

安利一个视频：https://www.bilibili.com/video/BV1X741127ZM?from=search——金牌爷的传授

反思总结

最大子数组和，上面给出了动态规划的解法，还可以使用递归的解法，时间复杂度也是 O(n)O(n)，但是空间复杂度却为 O(n)O(n)，所以最大子数组的最好解法还是动态规划。

动态规划还常常使用表格，缓存之前各个状态的解，通过空间换取时间，这个也是动态规划常用的技巧之一，但这却不是动态规划最难构思出来的地方，最难的还是设计每个状态步的决策策略，这才是动规的精髓。

另外，不是所有的问题都有动规的解法，比如目前全世界最难求解的旅行商问题，更复杂的多线路配送问题，都属于NP问题，很难找到动态规划的解法，但是一旦找到动规解法，它会将 O(n!)O(n!) 问题降为 O(n多项式)O(n多项式) 问题，收益也是巨大的！