Mrli
别装作很努力,
因为结局不会陪你演戏。
Contacts:
QQ博客园

时间序列概念及主要模型

2019/09/15 数学建模
Word count: 2,975 | Reading time: 14min

时间序列概念及主要模型

Q:什么是时间序列分析?
A:时间序列是按照时间顺序，按照一定时间间隔取得的一系列观测值
Q:怎样做时间序列分析?
A:时间序列分析尝试找出序列值在过去呈现的特征模式，假定这种模式在未来能够持续，进而对未来进行预测

时间序列三大特征

  • 序列相关性：当期的序列值和前期某个或某些序列值线性相关
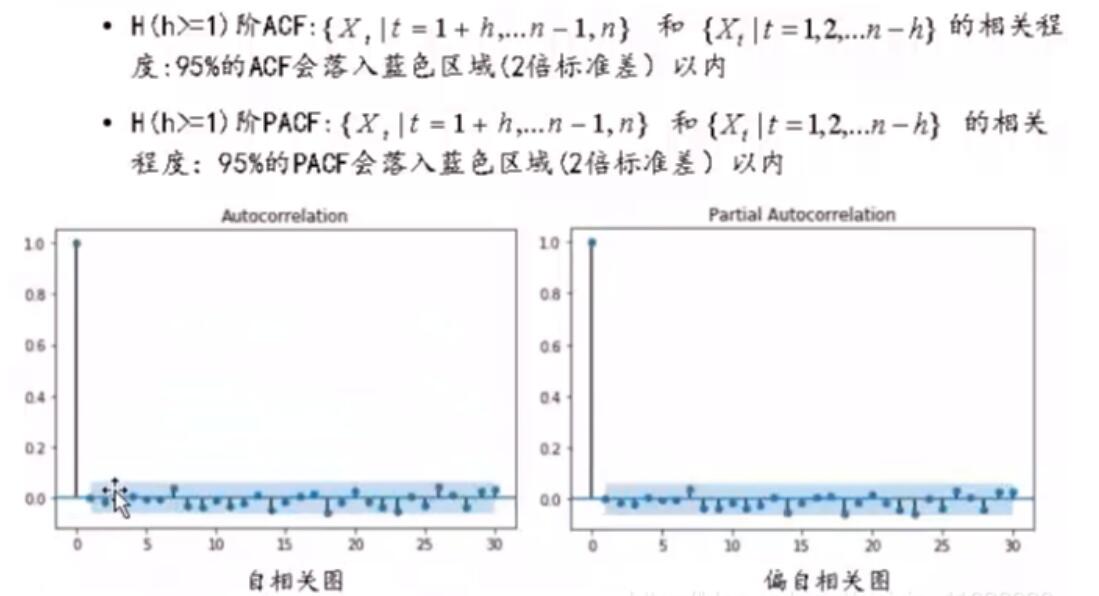
    √ 自相关系数（全相关系数）（ACF）：用来度量同一事件在不同时期之间的相关程度。ρh=r(h)r(0)\rho_{h}=\frac{r(h)}{r(0)}，其中r（h）为h期协方差函数，r（0）为方差
    √ 偏自相关系数（PACF）：度量去除中间变量影响后的相关程度。XtX_{t}和Xt−2X_{t-2}通过Xt−1X_{t-1}产生关联，PACF即为去除Xt−1X_{t- 1}的关联后两者的相关程度
  • 趋势性：序列整体上呈现单调性，如平稳，上涨或下跌
    • ARMA模型是平稳的时间序列模型，在建模前必须去除趋势性
  • 随机性：序列在一定程度上呈现不确定性
    • 模型并不能够捕捉到现实世界中的所有特征，总有一些噪声的存在，这些噪声叫做白噪声

时间序列模型预测方法：

算术平均法，移动平均法，加权移动平均法，指数平滑法，自回归法和移动平均法（ARIMA）

算数平均法：对时间序列的过去数据进行简单平均来进行预测
移动平均法(ARIMA)：不考虑远期的数据，仅考虑近期数据产生的影响。
加权移动平均法：给予近期数据较大的权重，远期数据较小的权重
指数平滑法：给予近期数据较大的权重，远期数据较小的权重，但是权重以指
数的形式适减
自回归法和移动平均法（ARIMA）:先对数据做了差分，之后再使用自回归滑动平均模型[^ARMA]模型。优点信息浪费最少，集趋势性，相关性和随机性于一身

基本概念

T时刻的时间序列值表示为XtX_t,T-1时刻的序列值表述为Xt−1X_{t-1}或者X[t−1]X[t-1]

一个时间序列可以表述为：{Xt∣t=1,2,3…n}\left\{X_{t} | t=1,2,3 \dots n\right\}

滞后算子BX,=Xt−1B X,=X_{t-1}

时间序列的差分:Xt−Xt−1X_{t}-X_{t-1}或者X[t]−X[t−1]X[t]-X[t-1]
一阶差分：Xt−Xt−1=Xt−BXt=(1−B)XtX_{t}-X_{t-1}=X_{t}-B X_{t}=(1-B) X_{t}
二阶差分：∇(∇Xt)=∇Xt−∇Xr−1=(Xt−Xt−1)−(Xt−1−Xt−2)=Xt−2Xt−1+Xt−2=(1−B)2Xt\nabla\left(\nabla X_{t}\right)=\nabla X_{t}-\nabla X_{r-1}=\left(X_{t}-X_{t-1}\right)-\left(X_{t-1}-X_{t-2}\right)=X_{t}-2 X_{t-1}+X_{t-2}=(1-B)^{2} X_{t}
k步差分：Xt−Xt−k=Xt−BkXt=(1−Bk)XtX_{t}-X_{t-k}=X_{t}-B^{k} X_{t}=\left(1-B^{k}\right) X_{t}

思考：
1.三阶差分如何表达？3步差分如何表达？
2.为什么要进行一阶差分？二阶差分？
3.为什么要进行k步差分？
4.阶次差分与步长差分的区别？

时间序列分类

Q:什么是序列平稳？

A:

1.E(Xt)=μE\left(X_{t}\right)=\mu，对于所有t而言，序列的期望为一常数，见图一

2.Var⁡(Xt)=σ\operatorname{Var}\left(X_{t}\right)=\sigma，对于所有t，序列方差为一常数，见图二

3.r(h)=Cov⁡(Xt,Xt−l)r(h)=\operatorname{Cov}\left(X_{t}, X_{t-l}\right)对于所有t以及h〉0，序列的协方差为是由h唯一决定的函数，即h阶的相关性只与h有关，与时刻t无关，如：{Xn,Xn+1,Xn+2,…,Xn},{X1,X2,X3,…,Xn+1−n]\left\{X_{n}, X_{n+1}, X_{n+2}, \ldots, X_{n}\right\},\left\{X_{1}, X_{2}, X_{3}, \ldots, X_{n+1}-n\right]与{Xh+5,Xh+6,Xh+7,…,Xn+5},{X6,X7,X8,…,Xn+6−h}\left\{X_{h+5}, X_{h+6}, X_{h+7}, \ldots, X_{n+5}\right\},\left\{X_{6}, X_{7}, X_{8}, \ldots, X_{n+6-h}\right\}的相关性一致

根据序列是否平稳，时间序列可以分为：

平稳序列：白噪声序列、AR（p）序列，MA（a）序列，ARWA（p.g）序列
非平稳序列：ARlMA（P.d.g）序列

平稳条件:

1.E(xt)=μE\left(x_{t}\right)=\mu序列的均值应该是一个常数，而不是随时间变化的函数。下图中左图满足要求，而右图的均值是随时间而变化的。

1

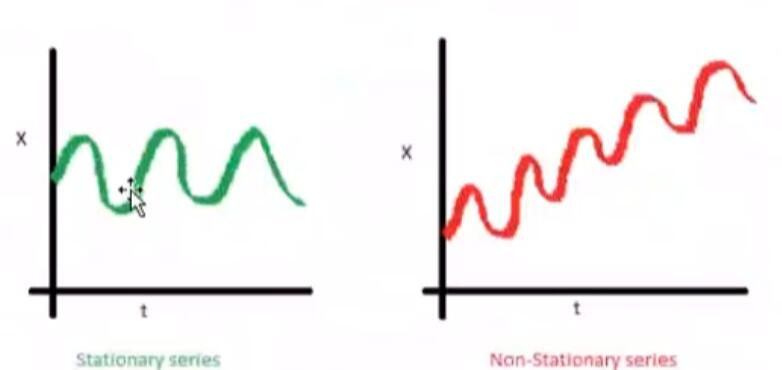
2.Var⁡(Xt)=σ\operatorname{Var}\left(X_{t}\right)=\sigma,序列的方差为一个常数，而不随时间的变化

2

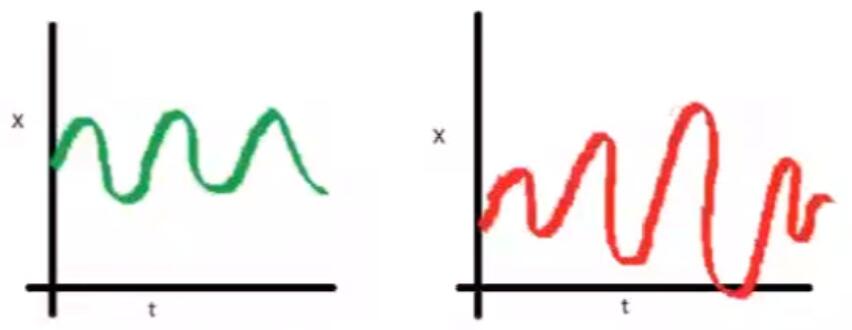
3.Cov⁡(yt,yt+k)=y0\operatorname{Cov}(y t, y t+k)=y 0,k,序列协方差的值只与时间间隔k有关，与时间t无关

3

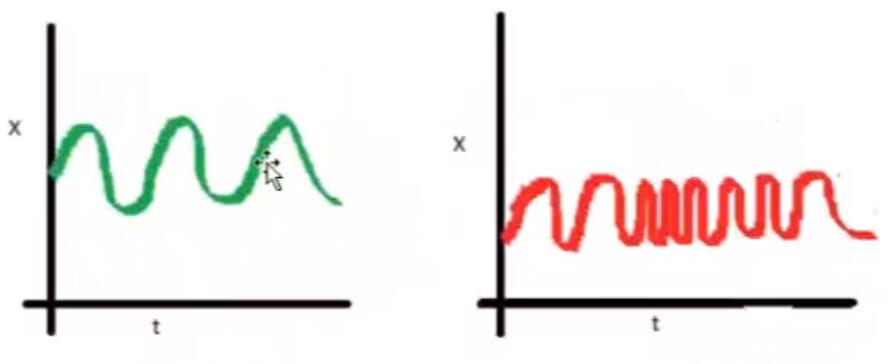
白噪声序列

(高斯)白噪声模型:Xt=et∣et∼WN(0,σ2)X_{t}=\mathrm{e}_{\mathrm{t}} | \mathrm{e}_{\mathrm{t}} \sim \mathrm{WN}\left(0, \sigma^{2}\right)
(高斯)白噪声就是一系列独立分布的正态序列：

  • 序列相关性：无
  • 趋势性：无
  • 随机性：是

白噪声的每一个时序点都是服从正态分布的

B

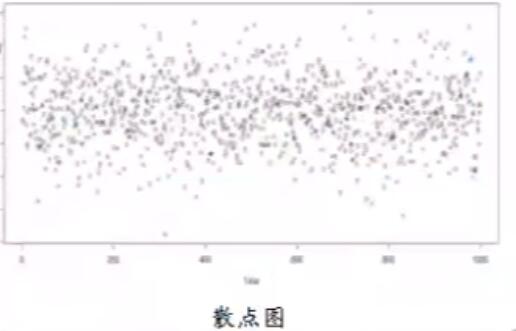
高斯白噪声散点图

序列无规律可循，在均值处反复震荡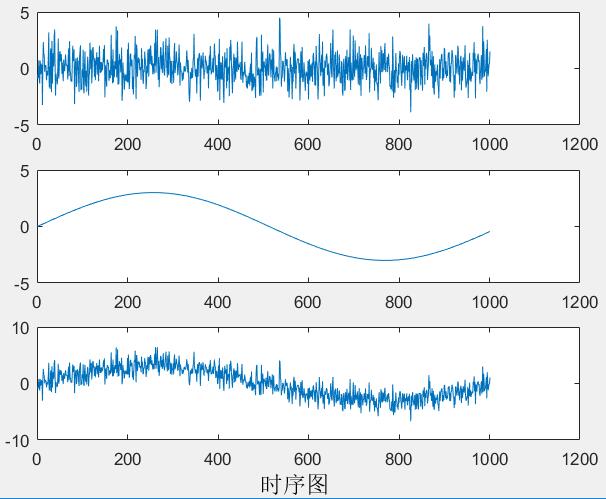高斯白噪声

1
2
3
4
5
6
7
8
9
10
11
clear,clc;
N=0:1000;
fs=1024;
t=N./fs;
y=3*sin(2*pi*t);
x=wgn(1,1001,2);	% wgn产生高斯白噪声
i=y+x;				% 给原有信号y叠加高斯白噪声
%i=awgn(y,2); 		% awgn在信号y中加入高斯白噪声。
subplot(3,1,1),plot(x);
subplot(3,1,2),plot(y);
subplot(3,1,3),plot(i);

自回归模型AR

▲AR§:

Xt=β1Xt−1+β2Xt−2+…+βpXt−p+etet∼WN(0,σ2)X_{t} = \beta_{1}X_{t-1}+\beta_{2} X_{t-2}+\ldots+\beta_{p} X_{t-p}+\mathrm{e}_{t} \quad \mathrm{e}_{t} \sim \mathrm{WN}\left(0, \sigma^{2}\right)

当前时刻的时序值可由其过去值的线性组合加上一个白噪声

建模的目的就是要搞清过去几期的历史值会影响当前值

模型特征：

  • 趋势性：无
  • 相关性：有
  • 随机性：有

▲AR（1）模型:

Xt=β1Xt−1+etX_{t}=\beta_{1} X_{t-1}+e_{t}

一阶自回归模型是最简单的自回归模型

该模型在t+1时的情形:Xt+1=β⊥Xt+et+1X_{t+1}=\beta_{\perp} X_{t}+e_{t+1}

自相关系数：ρ1=β1,ρ2=β12,…,ρk=β1k,k≥3\rho_{1}=\beta_{1}, \rho_{2}=\beta_{1}^{2}, \ldots, \rho_{k}=\beta_{1}^{k}, \mathrm{k} \geq 3
偏自相关系数：φ11=ρ1,φkk=0,k⩾2\varphi_{11}=\rho_{1}, \varphi_{k k}=0, k \geqslant 2

AR（1）的序列相关性：

  • ACF星现指数下降趋势
  • PACF在一阶处出现峰值，之后截断

B2

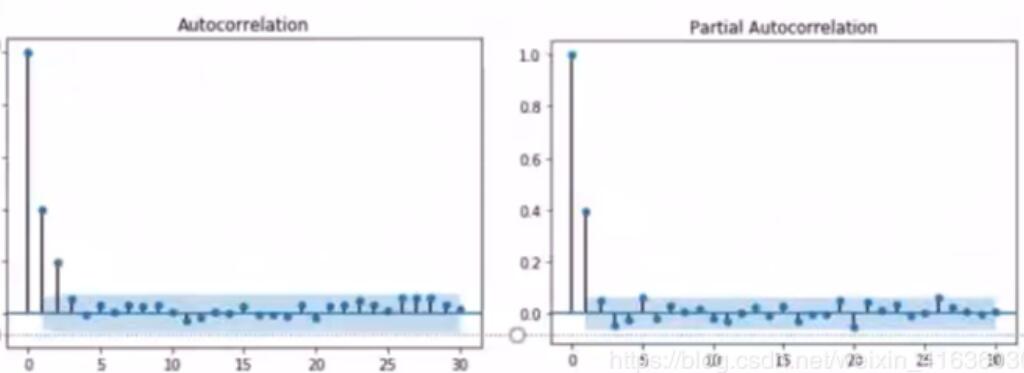
Q:如何识别自回归阶数

A:

  • PACF显示出剧烈地下降，并截断在P阶，而ACF呈指数下降趋势
  • PACF截尾的阶数即为AR模型的阶数

移动平均模型MA

▲MA(a):

Xt=et+β˙1et−1+β2et−2+…+βqet−qX_{t}=e_{t}+\dot{\beta}_{1} e_{t-1}+\beta_{2} e_{t-2}+\ldots+\beta_{q} e_{t-q} , et∼WN(0,σ2)e_{t} \sim W N\left(0, \sigma^{2}\right)

序列当前时刻的时序值是过去q阶白噪声的线性组合

建模的目的在于：

  • 找出过去几期的白噪声影响了当前值
  • 找出过去a期冲击效应对当前值的影响

模型特征：

  • 趋势性：无
  • 相关性：有
  • 随机性：有

▲MA（1）模型:

Xt=et+β1et−1X_{t}=e_{t}+\beta_{1} e_{t-1}

一阶移动平均模型是最简单的移动平均模型

该模型在t+1时的情形？Xt+1=et+1+β1etX_{t+1}=e_{t+1}+\beta_{1} e_{t}

​ MA（1）模型是利用t时刻的冲击变量值来预测将来

自相关系数：ρk=γkγ0={β11+β12,k=10k≥2\rho_{k}=\frac{\gamma_{k}}{\gamma_{0}}=\left\{\begin{array}{cc}{\frac{\beta_{1}}{1+\beta_{1}^{2}},} & {k=1} \\ {0} & {k \geq 2}\end{array}\right.
偏自相关系数：φkk={ρ1,k=1−ρ121−ρ12k=2−φk−1,k−1ρ11−φk−1,1ρ1k≥3\varphi_{k k}=\left\{\begin{array}{cc}{\rho_{1},} & {k=1} \\ {\frac{-\rho_{1}^{2}}{1-\rho_{1}^{2}}} & {k=2} \\ {\frac{-\varphi_{k-1, k-1} \rho_{1}}{1-\varphi_{k-1,1} \rho_{1}}} & {k \geq 3}\end{array}\right.

自回归滑动平均模型ARMA

▲ARMA（p,q）:Xt=β1Xt−1+…+βpXt−p+et+α1et−1+α2et−2+…+αqet−qX_{t}=\beta_{1} X_{t-1}+\ldots+\beta_{p} X_{t-p}+e_{t}+\alpha_{1} e_{t-1}+\alpha_{2} e_{t-2}+\ldots+\alpha_{q} e_{t-q}

ARMA（p,q）模型就是AR（p）和MA（q）模型的组合

ARMA模型是更普遍的一类模型

模型特征：

  • 趋势性：无
  • 相关性：有
  • 随机性：有

▲ARMA(1,1)：

通过查看自相关函数ACF和偏自相关函数PACF识别相关性
ACF呈指数下降趋势
PACF呈现指数下降趋势

B3

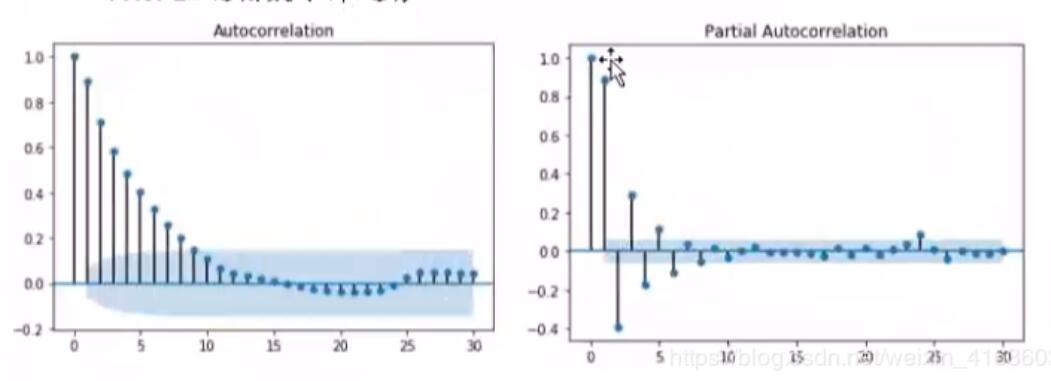
Q:如何识别一个ARMA的阶数p和q?

A:
1.由于ACF与PACF均呈现指数下降，判断阶数需要靠不断尝试
2.在模型的不同尝试中，通过选择AIC较小的为最优模型
AIC=2k+n∗ln⁡(RSSn)A I C=2 k+n * \ln (\frac{R S S}{n})k为参教数量，RSS为残差平方和

AR，MA，ARMA模型识别

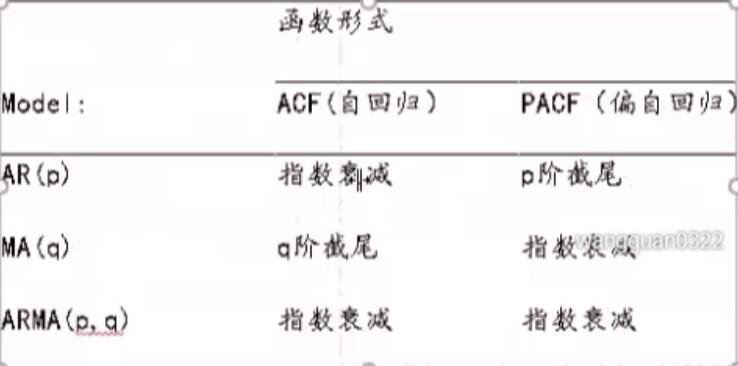
analyse

ARIMA模型

ARIMA是在ARMA基础上发展而来的更加综合性的模型，体现为：
■ 趋势性
■ 序列相关性
■ 随机性
ARIMA是不平稳的时间序列，不能直接用ARMA建模。ARIMA模型是在ARMA模型演变出来的，它实际上是先对数据做了差分，之后再使用ARMA模型；换句话说，ARIMA模型是先将非平稳数据变得平稳（用差分），之后再用ARMA模型处理平稳数据

ARIMA（1，1，0）的时间序列：
序列有很强的趋势性

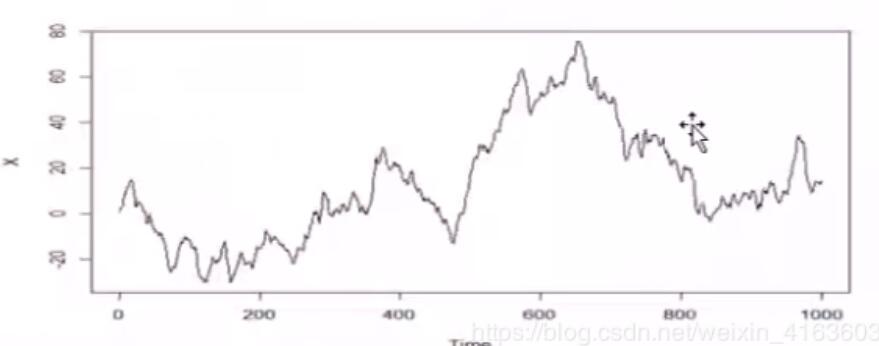
arima1

  • ARIMA（1，1，0）的序列相关性：
    ACF下降极其缓慢

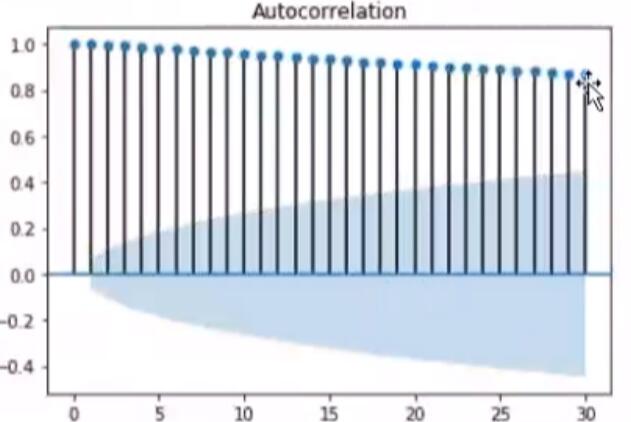
arima2

  • ARIMA（1，1，0）的序列图和ACF：

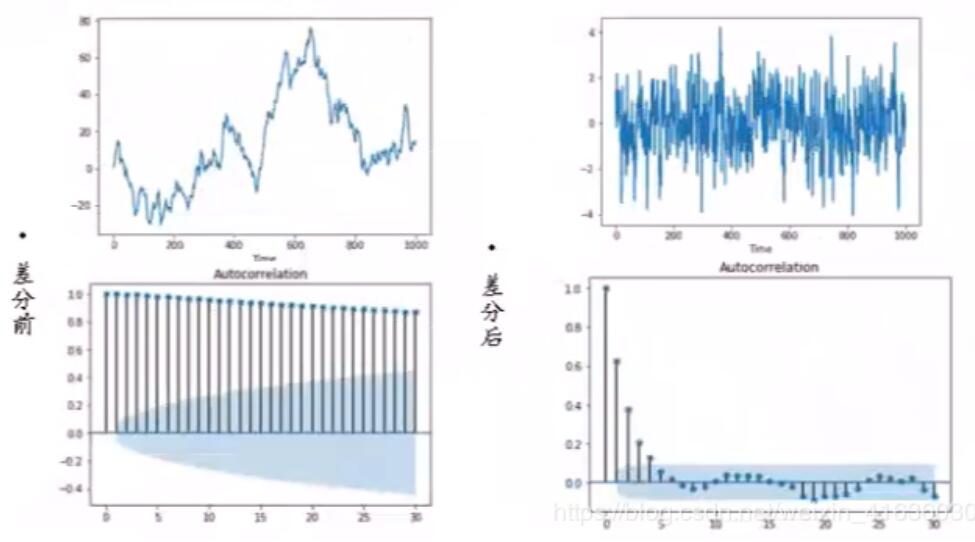
arima3

ARIMA(p,d,q)

  • ∇dXt=(1−B)dXt=Yt\nabla_{d} X_{t}=(1-B)^{d} X_{t}=Y_{t}
  • Yt=β1Yt−1+...+βpYt−p+et+α1et−1+α2et−2+…+αqet−qY_{t}=\beta_{1} Y_{t-1}+...+\beta_{p} Y_{t-p}+e_{t}+\alpha_{1} e_{t-1}+\alpha_{2} e_{t-2}+\ldots+\alpha_{q} e_{t-q}
  • 差分后的序列符合ARMA（p，g）

符号△为差分算子，∇dXt\nabla_{d} X_{t}代表d阶差分序列

一阶差分序列ΔXt=(1−B)∗Xt=Xt−Xt−1\Delta X_{t}=(1-B)^{*} X_{t}=X_{t}-X_{t-1}

预测的评价指标

ME（误差）：Mean（Actual-Predict）
MAE（绝对误差）：Mean（abs（Actual-Predict））
MAPE（百分比误差）：Mean（abs（Actual-Predict/Actual）
MSE（均方误差平方和）：Mean（（Actual-Predict）2）
RMSE（标准差）：Sqrt（Mean（（Actual-Predict）A2））

在模型选择方法上，通常会结合客户的建议以及其他的时间序列模型方法，选择某个评价指标，进而选择使该评价指标最小的模型方法

参考:https://blog.csdn.net/weixin_41636030/article/details/89115370

Author: Mrli

Link: https://nymrli.top/2019/07/29/时间序列概念及主要模型/

Copyright: All articles in this blog are licensed under CC BY-NC-SA 3.0 unless stating additionally.

< PreviousPost
Let's Encrypt安装配置nginx的SSL证书教程NextPost >
基础知识补充——白噪声、高斯白噪声
CATALOG
  1. 1. 时间序列概念及主要模型
    1. 1.1. 时间序列三大特征
    2. 1.2. 时间序列模型预测方法：
    3. 1.3. 基本概念
    4. 1.4. 时间序列分类
      1. 1.4.1. 白噪声序列
      2. 1.4.2. 自回归模型AR
        1. 1.4.2.1. ▲AR§:
        2. 1.4.2.2. ▲AR（1）模型:
      3. 1.4.3. 移动平均模型MA
        1. 1.4.3.1. ▲MA(a):
        2. 1.4.3.2. ▲MA（1）模型:
      4. 1.4.4. 自回归滑动平均模型ARMA
        1. 1.4.4.1. ▲ARMA（p,q）:Xt=β1Xt−1+…+βpXt−p+et+α1et−1+α2et−2+…+αqet−qX_{t}=\beta_{1} X_{t-1}+\ldots+\beta_{p} X_{t-p}+e_{t}+\alpha_{1} e_{t-1}+\alpha_{2} e_{t-2}+\ldots+\alpha_{q} e_{t-q}Xt​=β1​Xt−1​+…+βp​Xt−p​+et​+α1​et−1​+α2​et−2​+…+αq​et−q​
        2. 1.4.4.2. ▲ARMA(1,1)：
      5. 1.4.5. AR，MA，ARMA模型识别
      6. 1.4.6. ARIMA模型
    5. 1.5. 预测的评价指标