理解科学计算(numpy,pytorch)中的dim参数

😄理解numpy中array和pytorch中tensor的操作是开始科学运算的第一步!

首先明白维度的感念：

维度

我们通常能听到的都是2D, 3D，其实这边的D就是dimension的含义即维度。2D，我们通常理解为是平面，如我们最熟悉的直角坐标系就是平面坐标系，还有极坐标系。而3D呢，就是在平面的基础上增加了一维——高度，从而使平面的物体立起来了，同样3D也有耳熟能详的坐标系——3维坐标系。

更官方的解释呢：维度（Dimension），又称为维数，是数学中独立参数的数目。在物理学和哲学的领域内，指独立的时空坐标的数目。0维是一个无限小的点，没有长度。1维是一条无限长的线，只有长度。2维是一个平面，是由长度和宽度(或部分曲线)组成面积。3维是2维加上高度组成体积。4维分为时间上和空间上的4维，人们说的4维通常是指关于物体在时间线上的转移。（4维准确来说有两种。1.四维时空，是指三维空间加一维时间。2.四维空间，只指四个维度的空间。）四维运动产生了五维。

从哲学角度看，人们观察、思考与表述某事物的“思维角度”，简称“维度”。例如，人们观察与思考“月亮”这个事物，可以从月亮的“内容、时间、空间”三个思维角度去描述；也可以从月亮的“载体、能量、信息”三个思维角度去描述。这边的维度其实也可以理解为角度，从不同的方面去看待、确定一个事物。

所以代数上来说，维度其实是数学里在表示方面的一个重要的概念，它反映的是一个空间的本质性质。

科学计算中维度的概念

从二维点位置->编程中的坐标系

维度的考量主要集中在矩阵的运算上。首先我们来看一个元素：4，其实它就是一个点，可以被认为是0维的。但往往我们不会只有一个元素。我们最常见的是编程中的数组，如[1,2,3,4]，这个是由多个元素构成的，它的维度就是一维的，这个我们也比较好理解。

而二维是什么呢？我们能直观理解的二维是平面坐标系的那种：(1,3), (4,5)…即给一个x，一个y，那么在平面中就可以在直角坐标系下确定这个点（物）。现在我们规整下这些坐标点[ (1, 3), (4, 5) ]，从这个角度上离我们的矩阵，或是数组好像还是有点远。那么我们继续变形。

如果我们需要画出坐标系中有哪些点的话， 1.第一种做法就是跟上述一样，把点都存一个vector中[ (1, 3), (4, 5) ]，然后遍历，再在坐标系中点出。2.第二种呢，就是在坐标系中把所有的位置都列出来，如果有点存在就把它标出来，即跟我们列出迷宫地图一样，先把地图画出来，然后再把宝藏标出来。所以上述的两个点可以理解为。在给出了map[20][20]的地图上，(1, 3)和(4, 5)位置为true，即map[1][3] = 1, map[4][5] = 1，其他位置map[x][y] = 0，所以这样我们就从[(1, 3), (4, 5)]==> 用map形式表现出了这两个点，两者成功在二维上进行了转换。接下来我们就来分析这个二维的map。

数组，在编程中，我们都不陌生，如int arr[50][50]，虽然可以通过这个二维的数组，根据val的不同来表示三维的量，但是我们这边不把它这么理解，仅是当做bool arr[50][50]来理解维度上的概念。===>同样，面对numpy中的array我们也是这么个理解。

import numpy as np
import torch 
x = np.random.randint(2, size = (2,3))
print(x)

y = torch.randint(2, size = (2, 3))
print(y)
'''
[[0 1 1]
 [1 0 1]]
tensor([[1, 0, 1],
        [0, 0, 1]])
'''

我们从numpy的x上理解，这边是创建了一个2*3的矩阵，其中x[0][1], x[0][2], x[1][0], x[0][2]全1，其余为0，输入x.shape得到的结果是(2, 3)，有两项，跟我们从map的理解上是一致的，这个地图map拥有长和宽两个维度。

然后我们从编程中观察这个2*3的矩阵或是叫数组，可以发现x[a][b]第一个[]中的内容a范围是从0-1的，第一个[]中的内容b范围是从0-2的，0的话学编程的人都能很快的理解，而第二个的范围却不太那么肯定。为什么呢？因为它跟我们普通认知的直角坐标系不一致。下面我们把x画出来(不改变输出显示的形式，而是让坐标系去适应这种表现形式)。

坐标系

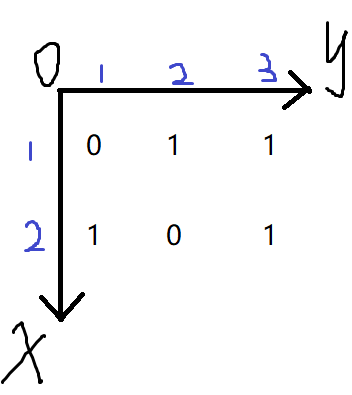
为什么是这样画的呢？首先明确的原则是，不改变输出显示的形式，而是让坐标系去适应这种输出形式，因此输出长啥样，我们坐标系只能去适应。由于我们碰到有x，有y的时候，习惯上把第一个出现的当作x，第二个当作y，所以就有了第一个[]为x，第二个[]为y。

好了，现在我们确定好坐标系长什么样了。接下来就是具体理解dim的含义了

编程中坐标系->科学计算中array的dim

想必大家在学习numpy或者torch的时候都被各种函数方法中的dim参数折磨过，感觉怎么理解都有问题，不敢自己使用。因此，这边就是解决，这些函数中的dim到底是怎么确定的

比如我们创建一个高维的array

A = torch.randint(2, size = (1,2,3,4))
'''
tensor([[[[0, 0, 1, 0],
          [1, 1, 0, 1],
          [0, 0, 0, 0]],
         [[0, 0, 1, 1],
          [1, 1, 1, 0],
          [0, 1, 0, 0]]]])
'''

举个我自己最初理解dim的笨方法：硬记x为第一维(dim = 0)， y为第二维(dim = 1)

实际上这种记法是比较低效的，最好的方法是我们怎么定义这个array就怎么记，比如我们这边创建的是一个size=(1, 2, 3, 4)，输出len(A.shape)为4，可以看到这就是个4维的tensor，那么我们顺理成章地就把把各个维度依次定义出来了。如dim = 0地指的就是size = 1的那层，dim = 1就是指size = 2的那层，依次类推。这样说可能有点抽象，因此我们回归简单的。

B = torch.randint(2, size = (3, 2))
print(B)
'''
tensor([[1, 0],
        [1, 1],
        [0, 0]])
'''

按照我们刚的定义，dim=0就是size=3的这一层，也就是我们坐标系中的X轴orX面。

好了，想必大家这个时候还不知道我在说什么。接下来就带大家来测试函数。

测试dim在函数参数中的定义

提前指出把：要注意函数介绍中dim指的是"沿着dim这个维度"or"删除、增加…dim这个维度(在dim这个维度上进行维度修改)"

规约计算

一般是指分组聚合计算，表现结果就是会进行维度压缩

sum

沿着dim累加元素

C = torch.randint(5, size = (2, 5))
print(C)
'''
tensor([[2, 3, 3, 4, 0],
        [1, 0, 2, 4, 4]])
'''
print(C.sum(dim = 0))
print(C.sum(dim = 1))
'''
tensor([3, 3, 5, 8, 4])
tensor([12, 11])
'''

可以看到sum就是比较典型的"沿着dim"的例子，当dim = 0时就沿着dim = 0即x轴进行累加，由于sum这个函数会进行维度的压缩，所以最后的结果为tensor([3, 3, 5, 8, 4])

cumprod

通过dim指定沿着某个维度计算累积

其他的函数还有cumsum、prod、sum，实际上两者是相同的，还有mean、median、var、std、min、max

#
x = torch.Tensor([
    [2,3,4,5,6],
    [9,8,7,6,5,]
])
print(torch.cumprod(x, dim = 0))
print(torch.cumprod(x, dim = 1))
'''
tensor([[ 2.,  3.,  4.,  5.,  6.],
        [18., 24., 28., 30., 30.]])
tensor([[2.0000e+00, 6.0000e+00, 2.4000e+01, 1.2000e+02, 7.2000e+02],
        [9.0000e+00, 7.2000e+01, 5.0400e+02, 3.0240e+03, 1.5120e+04]])
'''

# min
x = torch.Tensor([
    [2,3,4,5,6],
    [9,8,7,6,5,]
])
print(torch.min(x, dim = 0))
print(torch.min(x, dim = 1))
'''
torch.return_types.min(
    values=tensor([2., 3., 4., 5., 5.]),
    indices=tensor([0, 0, 0, 0, 1]) )
torch.return_types.min(
    values=tensor([2., 5.]),
    indices=tensor([0, 4]) )
'''

# mean
x = torch.Tensor([
    [2,3,4,5,6],
    [9,8,7,6,5,]
])
print(torch.mean(x, dim = 0))
print(torch.mean(x, dim = 1))
'''
tensor([5.5000, 5.5000, 5.5000, 5.5000, 5.5000])
tensor([4., 7.])
'''

索引、切片、连接

squeeze，unsqueeze

unsqueeze关键字：参数dim指定在第几个维度增加"[]"，以提升维度

squeeze: unsqueeze的逆操作，删除dim指定的维度

unsqueeze

D = torch.Tensor( [1, 2, 3, 4, 5] )
y = D.unsqueeze(dim = 0)
print(y, y.shape)
'''
tensor([[1., 2., 3., 4., 5.]]) torch.Size([1, 5])
'''
y = D.unsqueeze(dim = 1)
print(y.shape)
'''
tensor([[1.],
        [2.],
        [3.],
        [4.],
        [5.]])  torch.Size([5, 1])
'''

可以看到的是dim = 0的时候就是在dim = 0 维度上增加了一维，使得变成了[1, 5]。第二个是在dim=1的位置加了一维变成了[5, 1] （这也就是为什么很多书上会说其实就是在dim维度上加了1）

▲这个典型就是要区分： 在dim维度上 和 沿着dim维度了

squeeze

F = torch.Tensor( [ [0, 2, 3, 4], 
                    [22, 33, 44 ,55]
                  ])
y = torch.squeeze(F, dim = 0)
print(y, y.shape)
'''
tensor([[ 0.,  2.,  3.,  4.],
        [22., 33., 44., 55.]]) torch.Size([2, 4])
'''
y = torch.squeeze(F, dim = 1)
print(y, y.shape)
'''
tensor([[ 0.,  2.,  3.,  4.],
        [22., 33., 44., 55.]]) torch.Size([2, 4])
'''

这边变换不大的原因是因为dim上没有size=1可以删除

split

按(沿着)dim维度将tensor分成n个部分

x = torch.Tensor([
    [1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
    [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
])
print(x)
print(torch.split(x, 5, dim = 1))
# 指定划分列表，表示依次有1,2,3,4个长度 (总和得跟dim维度上元素个数相同)
print(torch.split(x, [1,2,3,4], dim = 1))
'''

tensor([[ 1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10.],
        [10.,  9.,  8.,  7.,  6.,  5.,  4.,  3.,  2.,  1.]])
        
(tensor([								# 可以看到这个是在x[:][6]的地方将tensor切成了两个
		[ 1.,  2.,  3.,  4.,  5.],
        [10.,  9.,  8.,  7.,  6.]
        ]), 
tensor([
        [ 6.,  7.,  8.,  9., 10.],
        [ 5.,  4.,  3.,  2.,  1.]
        ]))
        
(tensor([[ 1.],
        [10.]]), tensor([[2., 3.],
        [9., 8.]]), tensor([[4., 5., 6.],
        [7., 6., 5.]]), tensor([[ 7.,  8.,  9., 10.],
        [ 4.,  3.,  2.,  1.]]))
'''

unbind

删除某个维度后，返回所有切片组成的元组


x = torch.rand(1,2,3)
# x = torch.rand(size=(1,2,3))
print(x, x.shape)
out = torch.unbind(x, dim = 1)
print(out, len(out))
'''
tensor([
		[
            [0.3631, 0.6672, 0.9489],
            [0.4944, 0.1606, 0.6122]
		]
         ])	torch.Size([1, 2, 3])
         
(
    tensor([[0.3631, 0.6672, 0.9489]]), 		torch.Size([1, 3])
    tensor([[0.4944, 0.1606, 0.6122]])			torch.Size([1, 3])
)      2
'''
    
    
x = torch.Tensor([
        [[1,2,3,4,],
        [5,6,7,8],
        [9,10,11,12]],
    
        [[13,14,15,16],
        [17,18,19,20],
        [21,22,23,24]]
])
print(x, x.shape)
out = torch.unbind(x, dim = 1)
print(out, len(out))
print(out[0].shape)
'''
tensor([
        [[1,2,3,4,],
        [5,6,7,8],
        [9,10,11,12]],
    
        [[13,14,15,16],
        [17,18,19,20],
        [21,22,23,24]]
])										        torch.Size([2, 3, 4])
(tensor([
		[ 1.,  2.,  3.,  4.],
        [13., 14., 15., 16.]]), 
tensor([
		[ 5.,  6.,  7.,  8.],
        [17., 18., 19., 20.]]), 
tensor([
		[ 9., 10., 11., 12.],
        [21., 22., 23., 24.]])) 
删除dim = 1, 把size[1] = 3的tensor拆成了3个tensor
	不要记这个： 因为dim0为z轴， dim1为x轴， dim2为y轴，所以删除dim1就是删除x轴，最后得到的就是yOz平面
'''

cat、stack

通过关键字dim指定按哪个维度拼接

x = torch.randint(1, 100, size=(2,3))
print(x)
y = torch.randint(1, 100, size=(2,3))
print(y)
res = torch.cat((x, y), dim = 1)
print(res)
'''

tensor([[71, 56, 44],
        [64, 30, 87]])
tensor([[39, 56, 63],
        [68, 28, 65]])
tensor([[71, 56, 44, 39, 56, 63],
        [64, 30, 87, 68, 28, 65]])
'''

# 加强高维理解
x = torch.randint(1, 100, size=(2,3,4))
print(x)
y = torch.randint(1, 100, size=(2,3,4))
print(y)
res = torch.cat((x, y), dim = 1)
print(res)
'''
tensor([[[81, 79, 10,  8],
         [47, 30, 48, 35],
         [10, 57, 68, 88]],

        [[33, 51, 60, 97],
         [27, 14, 83, 51],
         [51, 54, 79, 65]]])
tensor([[[85,  9, 95, 95],
         [29, 99, 12,  8],
         [32,  8,  3, 84]],

        [[13, 24, 46, 20],
         [86, 83, 72, 10],
         [76, 33, 79, 48]]])
tensor([[[81, 79, 10,  8],
         [47, 30, 48, 35],
         [10, 57, 68, 88],
         [85,  9, 95, 95],
         [29, 99, 12,  8],
         [32,  8,  3, 84]],

        [[33, 51, 60, 97],
         [27, 14, 83, 51],
         [51, 54, 79, 65],
         [13, 24, 46, 20],
         [86, 83, 72, 10],
         [76, 33, 79, 48]]]) torch.Size([2, 6, 4])
dim=1即沿元素为3的方向上延伸，所以结果变成了6
	不要记：也可以理解为沿x轴方向
'''

官方文档： https://pytorch.org/docs/stable/generated/torch.cat.html?highlight=cat#torch.cat

总结

正确理解姿势

dim是指tensor在shape上的顺序(可以这么理解)，如x的shape是２ｘ３ｘ４，也就是[2, 3, 4]。故可以这样一一对应来。
比如dim = 1就是按具有3个元素的那个轴操作，从而不用死记硬背那些dim = 0是对列操作还是对行操作了。

强记三维

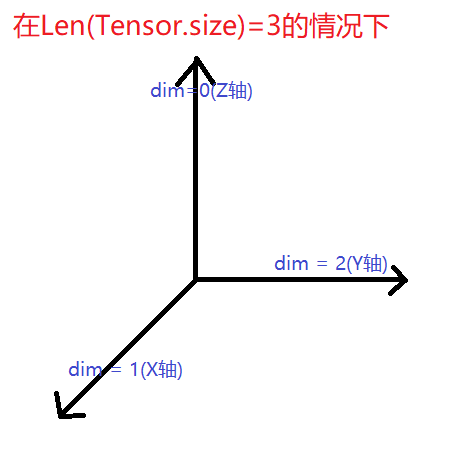
但还是不提倡强记，因为一旦高维就理解不了了。

附：

关于size的设置

在ones、rand等函数上，size = (2,3,4)，我们在C++数组中int arr[x][y][z]的理解是 $2*3$ 然后z为4，但实际上在科学运算中size = (2,3,4)的矩阵是有4个 $3*4$ 的矩阵叠加而成，这边是要区分的

>>> import numpy as np
>>> a = np.random.randint(1, 100, [2, 3, 4])
>>> a
array([[[26, 36, 31, 21],
        [74, 59, 79, 32],
        [77, 94, 81, 32]],

       [[72, 76, 85, 93],
        [66, 34, 80, 12],
        [99, 17, 98, 23]]])

x = torch.randint(1, 100, size=(2,3,4))
print(x)
print(x[1][2][3])		# 高度索引为1的, 在x = 2, y = 3的元素就是76
'''
tensor([[[63, 54, 57, 17],
         [78, 64, 76, 44],
         [96,  3, 59, 37]],

        [[86,  3, 92, 84],
         [89, 36,  8, 79],
         [10, 87, 15, 76]]])
tensor(76)
'''

x = torch.randint(1, 100, size=(2,3,4,2))
print(x)
'''
tensor([[[[29, 50],
          [50, 69],
          [95, 70],
          [21, 35]],

         [[58, 65],
          [15, 53],
          [96, 25],
          [11, 75]],

         [[12, 71],
          [36, 12],
          [71, 92],
          [87, 47]]],


        [[[43, 89],
          [88, 22],
          [61, 56],
          [47, 97]],

         [[71,  7],
          [44, 88],
          [54, 32],
          [15, 65]],

         [[96, 22],
          [90, 78],
          [30, 85],
          [65, 57]]]])
'''

关于如何看图

import numpy as np
res = np.uint8(np.random.rand(5,5,3) * 255)
print(res)
plt.imshow(res)
plt.show()
"""
[[[ 19 228 231]
  [106  28 252]
  [191  98 139]
  [171  71 202]
  [105 101  93]]

 [[155 232 228]
  [ 89 119  13]
  [142 158 200]
  [226 169  55]
  [137 187 249]]

 [[202 217  96]
  [214  44 133]
  [144 253 213]
  [ 82   4  28]
  [172 242 238]]

 [[106 103  68]
  [236 252  63]
  [ 53  49  66]
  [ 48 121  62]
  [ 64  61 209]]

 [[158  80 221]
  [220  12 199]
  [214  40   3]
  [169 142 144]
  [140 112 148]]]
  """

画图效果如下：

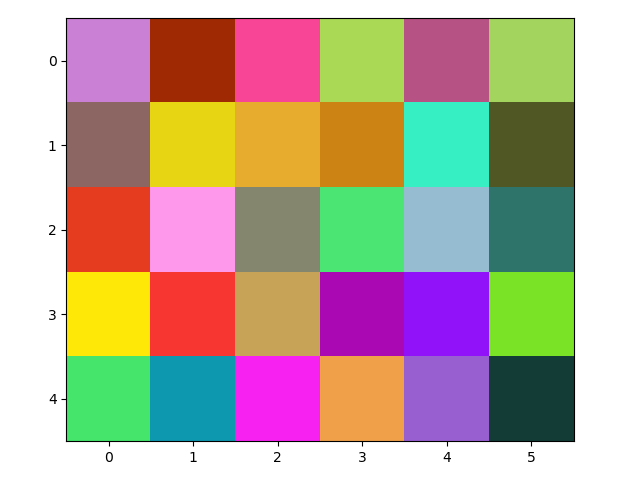
可以得到的结果是针对np.random.rand(5,5,3)来说，三个通道被列成了三列，因此每一列就是一个通道。

res = np.uint8(np.random.rand(5,5,3) * 255)
[[[ 19 228 231]
  [106  28 252]
  [191  98 139]
  [171  71 202]
  [105 101  93]]
  
res = np.uint8(np.random.rand(5,6,3) * 255)
[[[217 210 138]
  [  1 148  10]
  [ 25 231 128]
  [158 216  73]
  [220 208 165]
  [ 73 119 122]]
# 单元中竖着的行数表示了图片的长，可以看到横着的长是6
# 而有多少个单元就以为着图片的宽， 可以看到竖着的宽是5==> 所以第几个单元意味着第几行
# 所以[0][5][0]=73标志着右上角那一块绿色的第一个通道的值
 
# 可以设置后再绘图看看是不是右上角的图块变成白色的了
res[0][5][0] = res[0][5][1] = res[0][5][2] = 255
print(res[0][5][0])

总结： RGB图像的shape：(H, W, C)

pytorchAPI:

https://pytorch.org/docs/stable/torch.html#torch.arange